OPTIONS/OPTIONS CONTRACTS
An option is the right to choose a particular action among alternatives. A financial option contract is the right, but not the obligation, to buy or sell a specified amount of an asset at a specified price, for a specified time period. The term is most often associated with stock, but options are available on other assets. There are also a number of other financial instruments, such as warrants and callable or convertible bonds, which include option features. Options and instruments with option features are sometimes called derivatives, or contingent claims, since the value of the instrument is derived from or contingent upon the value of some underlying asset. Options have become important tools for managing risk. More recently, financial engineering has produced an array of innovative financial instruments and strategies that employ options or exhibit option characteristics.
An option contract may be a "put" or a "call." The buyer, or "holder" of a call has the right to buy (call in), the underlying asset. The holder of a put has the right to sell (put onto someone else), the underlying asset. Although the underlying asset, the price of the trade, and the time period are fixed, the holder of the option is not obligated: the alternatives of choice are to "exercise" the option or to let the option expire. The seller, or "writer," of a put (call) is, however, obligated to buy (sell) at the strike price if the buyer decides to exercise the option. The fixed price at which the purchase or sale can be executed is called the "strike price" or the "exercise price." Since the right to decide is valuable, the buyer of an option purchases the option at a price referred to as the "premium." Options may be "European" or 'American,"' but this label does not refer to where the option is traded. Rather, European options may be exercised only at expiration, while the more prevalent American option may be exercised at any time on or before expiration.
Conventional option contracts are available over-the-counter from put and call dealers, who provide individualized option contracts. In 1973, however, the Chicago Board Options Exchange began trading standardized options contracts. These exchange-traded or "listed" options are less flexible and are available only on certain assets, but are easier and cheaper to trade, provide greater trading depth and have an active secondary market. Standardized options are now traded on several exchanges and account for the bulk of options trading. Listed options are available on many common stocks, various foreign currencies, and several stock indexes. Listed options are also available on futures contracts for agricultural commodities, precious metals, foreign currencies, and interest rates.
An additional attraction of listed options is that there is no risk of seller default. Performance is guaranteed by the Options Clearing Corporation (OCC). The OCC enters each transaction, becoming a buyer to the seller and a seller to the buyer, but maintaining a zero net position. When an option is exercised before expiration, the OCC will deliver on the option. In order to maintain the zero balance, the OCC will at the same time exercise the option contract with a seller. In this case the exercise is randomly assigned to a broker or dealer, who will in turn assign the exercise to a client who has written the contract. The OCC charges a small fee on each transaction for providing this service.
TYPES OF OPTIONS
The exact terms of standardized option contracts vary with the nature of the underlying asset. For options on common stock, the contract size is 100 shares. Not all strike prices are traded. Strike prices are set by the exchange, most often at multiples of $5.00. The exchange will begin trading options of a given expiration at a strike price or prices that are close to the market price. If the price of the stock changes, however, the exchange will initiate trading in contracts at other strike prices. Eventually, there may be many contracts traded with the same expiration but different strike prices. Strike price and contract size are adjusted for stock splits, and for stock dividends of more than 10 percent, using the split factor, e.g., a three-for-two stock split would result in an option on 150 shares at two-thirds of the original strike price. Cash dividends have no effect on the option. The maturity of stock options is usually identified by the month of expiration, with all options expiring on the Saturday following the third Friday of the month. Options with maturities up to two years, called "long-term equity anticipation securities" (LEAPS) are available on some blue-chip stocks. Most stock options have maturities of eight months or less, however, and fall into one of three expiration cycles: (1) January, April, July, and October; (2) February, May, August, and November; or (3) March, June, September, and December. Generally, options with expiration in the next two calendar months, plus the next two closest months in the expiration cycle, are available.
Option terms on other assets are set similarly—options on wheat, for instance, call for delivery of 5,000 bushels of a stated type and quality at a stated location. Foreign currency options are written on a set amount of the foreign currency, with expiration on the Saturday before the third Wednesday of the month. Maturities available include the next two months, and March, June, September, and December. Interest rate options are written on a specific amount (usually $100,000) of a specific U.S. Treasury note or bond. They are available with original maturities of three and six months, but normally options on a given instrument are traded for only one expiration cycle. Rather than introducing new options on the same securities, they are replaced with options on recent issues.
Options on indexes include broad stock market indexes and industry-specific indexes. Expiration dates are similar to those of stock options. An importance difference here is the nature of delivery. The contract is written on 100 units of the underlying index. Since it would be impractical or even impossible for writers to deliver the exact assets and proportions specified in the index, cash settlement is used. At exercise, the writer delivers cash equal to 100 times the (positive) difference between the index value and the strike price. Another important difference is that an order to exercise is executed after the close of trading at the ending price, rather than at the time and the price when the order is given. Although the cash settlement is a desirable feature, it may increase the price volatility of the underlying stock. This occurs because institutional investors with large portfolios use index options to hedge against losses, or to take advantage of small price imbalances. As the options approach expiration, attempts to restructure these positions cause large transactions with attendant price swings.
The options discussed so far are based on the spot price, the price for immediate delivery of the asset. A futures contract, however, calls for delivery of the underlying asset at a fixed price at some time in the future. An important difference between an option and a futures contract is that the buyer of a futures contract assumes the obligation to perform. An option on a futures contract, or "futures option," provides the option feature based on the trading price at some time in the future. Futures options are available on agricultural commodities, precious metals, fixed-income securities (called "interest rate options") and stock indexes. Trading volume in futures options sometime exceeds trading volume in the spot contract. The exact maturities and expiration dates vary among the underlying assets traded.
OPTION PAYOFFS
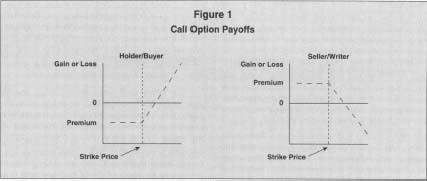
The key to the analysis of gains and losses on option positions is that the buyer of the option has the right, but not the obligation, to exercise. The buyer would not exercise the option if exercise would result in a loss. For this reason, many options are never exercised and simply expire. This also implies that the maximum possible loss for the buyer, and the maximum gain for the writer, is the premium. Consider a listed call option on XYZ stock with a strike price of $30, purchased for a premium of $200, which is about to expire. The net payoffs at expiration for both the writer and the buyer are given in Table 1 for a range of market values of the underlying stock. At any price below $30, the buyer will not exercise the call option because to do so would be to buy the stock above market—the option is said to be "out of the money." Expiration is preferable to exercise because by not exercising the buyer limits the loss to the premium paid to obtain the option, in this case $200. At $30, the option is "at the money," and the buyer is indifferent about exercise. Above $30, the buyer could exercise the option and buy the stock at a price below market—the option is "in the money." Note that this may still result in a net loss, since the premium must be deducted. The loss would be higher, however, if the option was not exercised. At $32, the buyer breaks even, and any further increases in the value of the stock result in proportional ($100 for each $1 change) net gains limited only by the maximum stock price. The payoffs of the buyer and the writer are always a mirror image, as depicted in Figure 1. The writer thus has a maximum gain of $200, and an indefinite maximum loss.
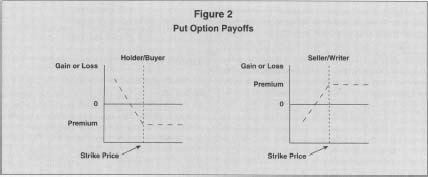
This same type of analysis can be applied to the payoffs from a put, as shown in Figure 2 for a put with
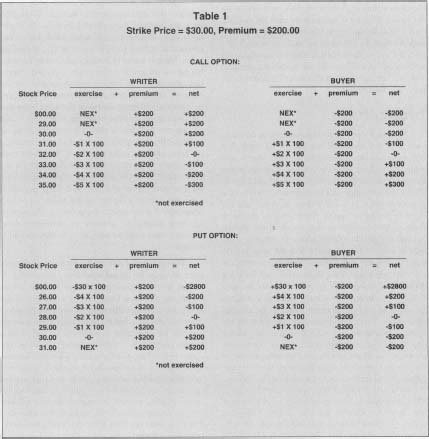
Strike Price=$30.00, Premium = $200.00
| CALL OPTION: | ||||||
| WRITER | BUYER | |||||
| Stock Price | exercise | + premium | = net | exercise | + premium | = net |
| $00.00 | NEX* | +$200 | +$200 | NEX* | -$200 | -$200 |
| 29.00 | NEX* | +$200 | +$200 | NEX* | -$200 | -$200 |
| 30.00 | -0- | +$200 | +$200 | -0- | -$200 | -$200 |
| 31.00 | -$1 X100 | +$200 | +$100 | +$1 X100 | -$200 | -$100 |
| 32.00 | -$2X100 | +$200 | -0- | +$2X100 | -$200 | -0- |
| 33.00 | -$3X100 | +$200 | -$100 | +$3X100 | -$200 | +$100 |
| 34.00 | -$4X100 | +$200 | -$200 | +$4 X100 | -$200 | +$200 |
| 35.00 | -$5X100 | +$200 | -$300 | +$5X100 | -$200 | +$300 |
| "not exercised | ||||||
| PUT OPTION: | ||||||
| WRITER | BUYER | |||||
| Stock Price | exercise | + premium | = net | exercise | + premium | = net |
| $00.00 | -$30x100 | +$200 | -$2800 | +$30x100 | -$200 | +$2800 |
| 26.00 | -$4X100 | +$200 | -$200 | +$4X100 | -$200 | +$200 |
| 27.00 | -$3X100 | +$200 | -$100 | +$3X100 | -$200 | +$100 |
| 28.00 | -$2X100 | +$200 | -0- | +$2X100 | -$200 | -0- |
| 29.00 | -$1 X100 | +$200 | +$100 | +$1 X100 | -$200 | -$100 |
| 30.00 | -0- | +$200 | +$200 | -0- | -$200 | -$200 |
| 31.00 | NEX* | +$200 | +$200 | NEX* | -$200 | -$200 |
| "not exercised | ||||||
Call Option Payoffs
OPTION STRATEGIES
The payoffs to various option strategies involving writing or buying combinations of puts, calls, and other assets can also be analyzed by combining the payoffs at various prices. A "straddle" is the combination of a put and a call on the same stock with the same strike price and expiration. For a buyer, a straddle will produce a loss of the two premiums if the price of the stock is at the strike price. If the price moves far enough away from the strike price in either direction, one of the options becomes in the money. The buyer will realize a gain if the price of the stock moves far enough away from the strike price, either up or down, so that the gain on exercise of the in-themoney option will more than equal the premiums. The opposite straddle position—sale, or "shorting" both a put and a call will result in mirror image payoffs. Variations on a straddle include strips (two puts and one call) and straps (two calls and one put). Spreads involve combination of calls or puts on the same underlying stock, but with differing strike prices or expirations.
A position involving only the option itself is called a naked option, while an option position combined with a long position in the underlying stock is called a covered option. Sales of covered calls, the sale of a call on a stock being held by the investor, has been a popular strategy. The seller of the covered call will lose the possibility of capital gains, but will receive additional income from the premium. This strategy would be appropriate if the seller does not expect a price increase, or planned to eventually sell the stock at the call price. Purchase of a put on a stock held long is termed a "protective put." The value of the put will increase as the stock price drops, so that the holder has reduced or "hedged" the potential loss.
Use of options is not limited to individual investors. Index options are widely used as a portfolio
Put Option Payoffs
RISK IN OPTION TRADING
There is no definitive answer to the question of the riskiness of option trading. As shown in Figure 1, the possible outcomes vary widely, and the strategy being followed must also be considered. Sale of a naked put or call exposes the writer to extreme losses, whereas purchase of the call or put has sharply limited loss possibilities. Covered options present limited risk, and protective puts or portfolio hedging are meant to reduce risk. There is no doubt, however, that some options trades can present significant risk. One reason for the popularity of options as investment vehicles is that they provide leverage. For the amount of the premium, the buyer "controls" 100 shares of stock, so that a $ 1 change in the value of the stock underlying and in-the-money option results in a much larger change in the premium. Because of the inherent risk, the OCC requires to option writer to post and maintain margin.
OPTION PRICING
Option pricing refers to the size of the premium. There are financial models of option premiums, such as the Black-Scholes Model, that attempt to specify the price on a quantitative basis. The largest influence on the premium is the relationship between the strike price and the market price of the underlying asset. The value of a call will be positively related, and the value of a put negatively related, to the market price of the underlying stock. For a given market price, the value of a call will be negatively related, and the value of a put positively related, to the strike price. Even if the strike price is above the market value of a call, or below the value of a put, the option will have value. This value is based on the possibility that the stock price will change enough to put the option in the money. Because the possibility that the option will become in the money is greater, the greater the volatility of the stock price, the premium for both a put and a call will be positively associated with the volatility of the underlying stock price. Interest rates are positively related to the premium because the leverage effect is more attractive in times of high interest rates.
The option itself has a positive value, and this value is greater the longer the time to expiration. Because of the value of time to expiration, few investors exercise options before expiration, but will instead sell the option. Option sellers can exit the position by engaging in an offsetting trade of purchasing the same option, which results in a canceling of the investors' position on the books of the OCC. Since there is no adjustment for dividends, which have a tendency to decrease stock price, the value of a call is negatively related, and the value of a put is positively related, to the dividend yield of the stock. As an exception to the general avoidance of early exercise, if a dividend is to be recorded before expiration, investors may wish to exercise calls to capture the dividend.
The relationship between the price of a put and the price of a call is
referred to as the
"put-call parity"
relationship. At maturity, a protective put will have a value equal to
the greater of the strike price or the stock price. An investor could,
however, purchase a call on the same stock at the same strike price and
expiration, and invest enough in
U.S. Treasury bills
(T-bills) to equal the strike price at expiration. At expiration, this
portfolio also has a value equal to the greater of the strike price or the
stock price. Since both of these positions have the same outcome, they
should have the same price or
arbitrage
is possible. Therefore,
where
C
= the call premium,
X
= the strike price,
(1 +
r
f
)
-T
= the
present value
factor for an amount invested at time
T
in T-bills at rate
r
f
,
S
= the stock price,
P
= the put premium.
ASSETS WITH OPTION FEATURES
Analysis of financial instruments with implicit or explicit option features can proceed by decomposing the instrument into a nonoption instrument plus an option or options. This separation provides a different perspective that may allow new insights into value. Most bonds, for instance, are "callable." This means that the bond can be repurchased by the issuer for the price of the bond plus a "call premium." The call feature is simply a call option held by the issuer. A callable bond can be analyzed as a purchase of a noncallable bond, plus the sale of a call on the bond—a covered call position in the bond. The value of a call feature would be affected by the same factors affecting other call options.
Rights arise in stock offerings and are sometimes associated with the
preemptive right of common stockholders to maintain their proportional
ownership of the firm. The existing shareholders of the firm are given one
right for every share that they own. Purchase of one share of the new
stock then requires
R
rights plus
$S
e
.
$S
e
is set at a value below the expected post-offering stock price
$S
p
. The
R
rights required for subscription then have a value
$S
p
—$S
e
, so that the value of one right will be:
There is a market for rights, and investors who do not wish to subscribe or who have odd numbers of rights may capture their value. The lifetime of rights is typically short, and they may be considered as options on the to-be-issued shares.
Warrants are options to buy a fixed number of newly issued shares at a fixed price, written by the firm. They often are included in bond offerings as "sweeteners" in order to make an issue more attractive, or in executive compensation. They typically have an extended lifetime, some even being perpetual, and originally are "deep" out of the money, carrying an exercise price well above market. The value of a warrant would be affected by the same factors affecting other call options.
Convertible bonds may be converted into common stock at some fixed ratio or face value per share. The conversion feature is in essence a call option on the common stock, and convertible bonds are sometimes analyzed as the combination of a bond and an option. A convertible will be valued at the higher of its value as a straight (i.e., nonconvertible) bond, or its conversion value as the underlying stock, plus an added premium for the value of the call option feature.
Financial engineering is the term applied to the creation of innovative financial instruments, and the options feature has been widely used in this activity. Analysis of the instruments often requires sophisticated mathematical treatment. Some of these instruments are individualized, while others are traded to varying degrees. These traded instruments include putable bonds, certificates of deposit with payoffs based on various indexes, and LYONS (zero coupon, convertible, callable, and putable bonds).
SEE ALSO : Call and Put Options ; Options Clearing Corporation
[ Davld E Upton ]
FURTHER READING:
Bodie, Zvi, Alex Kane, and Alan J. Marcus. Investments. 4th ed. Boston: Irwin/McGraw-Hill, 1999.
Chance, Don M. An Introduction to Derivatives. 4th ed. Fort Worth, TX: Dryden Press, 1998.
Kolb, Robert W. Futures, Options, and Swaps. 3rd ed. Malden, MA: Blackwell Publishers, 1999.
Reilly, Frank K., and Keith C. Brown. Investment Analysis and Portfolio Management. 5th ed. Fort Worth, TX: Dryden Press, 1997.
Comment about this article, ask questions, or add new information about this topic: