CAPITAL ASSET PRICING MODEL
(CAPM)

The capital asset pricing model (CAPM) is a mathematical model that seeks to explain the relationship between risk and return in a rational equilibrium market. Developed by academia, the CAPM has been employed in applications ranging from corporate capital budgeting to setting public utility rates. The CAPM provides much of the justification for the trend toward passive investing in large index mutual funds.

William Sharpe, John Lintner, and Jan Mossin simultaneously and independently developed the CAPM. Their research appeared in three different, highly respected journals during the period of 1964-66. When the CAPM was first introduced, the investment community viewed the new model with suspicion, since it seemed to indicate that professional investment management was largely a waste of time. It was nearly a decade before investment professionals began to view the CAPM as an important tool in helping investors understand risk.

The key element of the model is that it separates the risk affecting an asset's return into two categories. The first type is called unsystematic, or company-specific, risk. The long-term average returns for this kind of risk should be zero. The second kind of risk, called systematic risk, is due to general economic uncertainty. The CAPM states that the return on assets should, on average, equal the yield on a risk-free bond held over that time plus a premium proportional to the amount of systematic risk the stock possesses.

RISK AND THE CAPM

The treatment of risk in the CAPM refines the notions of systematic and unsystematic risk developed by Harry M. Markowitz in the 1950s. Unsystematic risk is the risk to an asset's value caused by factors that are specific to an organization, such as changes in senior management or product lines. For example, specific senior employees may make good or bad decisions or the same type of manufacturing equipment utilized may have different reliabilities at two different sites. In general, unsystematic risk is present due to the fact that every company is endowed with a unique collection of assets, ideas, personnel, etc., whose aggregate productivity may vary.

A fundamental principle of modern portfolio theory is that unsystematic risk can be mitigated through diversification. That is, by holding many different assets, random fluctuations in the value of one will be offset by opposite fluctuations in another. For example, if one fast food company makes a bad policy decision, its lost customers will go to a different fast food establishment. The investor in both companies will find that the losses in the former investment are balanced by gains in the latter.

Systematic risk is risk that cannot be removed by diversification. This risk represents the variation in an asset's value caused by unpredictable economic movements. This type of risk represents the necessary risk that owners of a firm must accept when launching an enterprise. Regardless of product quality or executive ability, a firm's profitability will be influenced by economic trends.

In the capital asset pricing model, the risk associated with an asset is measured in relationship to the risk of the market as a whole. This is expressed as the stock's a (beta), or correlation to the market average. The returns of an asset where 13 = I will, on average, move equally with the returns of the overall market. Assets with β < I will display average movements in return less extreme than the overall market, while those with a > I will show return fluctuations greater than the overall market. Mathematically, (is defined as the covariance of an asset's returns divided by the variance of the market's return. The market's return is most often represented by an equity index, such as Standard and Poor's 500 or the Wiltshire 5000. These large equity indexes are commonly viewed as bench-marks against which a securities performance is judged.

The preceding paragraphs are summarized in the following equation:

Where:
K _i = the required return on asset i
R _f = risk-free rate of return on a U.S. Treasury bill
β _i = beta coefficient or index of non-diversifiable risk for asset i
k _m = the return on the market portfolio of assets

ASSET RETURNS IN THE CAPM

The CAPM models return to an asset by the following three guidelines. First, all assets must have an expected return of at least the return to a risk-free bond (except for rare assets with (3 < 0, which will be discussed below). The rationale is that any risky asset must be expected to return at least as much as one without risk or there would be no incentive for anyone to hold the risky asset.

Second, there is no expected return to taking unsystematic risk since it may easily be avoided. Diversification is simple, does not affect the economics of the assets being held, and only helps the investors holding the assets. Therefore, there is no compensation inherent in the model for accepting this needless risk by choosing to hold an asset in isolation.

Finally, assets that are subject to systematic risk are expected to earn a return higher than the risk-free rate. This premium should be incremental to the risk free rate by an amount proportional to the amount of this risk present in the asset. This risk cannot be diversified away and must be borne by the investor if the assets are to be financed and employed productively. The higher the systematic risk, the higher the average long-term return must be for the holder to be willing to accept the risk.

The market risk premium was reported by R. Ibbotsen and R. Sinquefield to average about 6.1 percent. This amount is modified by the (3 which scales it up or down depending on the asset's sensitivity to market movements. Interestingly, some assets have a negative premium. This is because their (3 is less than zero, meaning the asset's expected return is less than the risk-free rate. Assets with negative returns are those that actually hedge against general economic risk, doing well when the economy performs poorly. Examples of this type of asset are precious metals.

The Security Market Line (SML), which has the following equation, may summarize the preceding discussion:

Where:
E[R _i ] is the expected return to asset i
R _f is the risk free rate of return
β _im is asset i 's market Beta
E [ R _m — R _f ] is the expected market risk premium

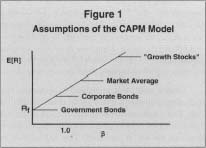
Graphically, the SML may be represented by the graph in Figure 1.

ASSUMPTIONS OF THE CAPM

The CAPM draws conclusions from a variety of assumptions. Some are vital to its premise, others cause only minor changes if they are untrue. Since the early 1970s much research into the plausibility and effects of weakness in these assumptions has been conducted by academia. The assumptions that form the basis for the CAPM are:

• Investors measure asset risk by the variance of its return over future periods. All other measures of risk are unimportant.
  
• Investors always desire more return to less, and they are risk averse; that is, they will avoid risk if all else is equal.
• There are no restrictions on the borrowing and lending of money at the risk-free rate of interest.
• All possible investments are traded in the market and are available to everyone, the assets are infinitely devisable, and there are no restrictions on short selling.
• The market is perfectly efficient. That is, every investor receives and understands the same information, processes it accurately, and trades without cost. There is no consideration of the effects of taxation.

EMPIRICAL TESTS OF THE CAPM

Two early tests of the CAPM revealed that the model was conceptually sound except that the Security Market Line intercept was estimated to be approximately 3 to 4 percent higher than the risk-free rate. This is consistent with a CAPM model where money cannot actually be borrowed at the risk-free rate.

R. Roll wrote a famous article in which he argued that tests of the CAPM are inherently impossible. The article is quite technical, but its basic point is the following. Since no one can observe the true market portfolio, only a proxy index, and since no one can actually observe expected returns, only average realized ones, it is impossible to know whether the correct relationship is actually being tested.

More recent tests of the CAPM show that there are many apparent shortcomings of the strict interpretation of the model. Examples include seasonal fluctuations (such as unusually high returns for some companies in January), and different average returns on Friday and Monday from that of other days of the week. In addition, some analysts have argued that stock returns are more closely related to the book value and total variability of the stock, rather than a beta calculated using a market index.

Others argue that many apparent inconsistencies can arise in the CAPM because a capital weighted index (such as the S&P 500) may not be an appropriate proxy for the market portfolio. This is especially true if the assumptions regarding short sales and risk free borrowing are violated.

EXTENSIONS OF THE CAPM

In 1976, S. Ross published a different model, the Arbitrage Pricing Theory (APT), which avoids the need for specifying a market portfolio. Although this model is generally believed to be more powerful than the CAPM, it is less intuitive and more difficult to implement. In the APT, an asset's return is related to multiple economic factors instead of the market portfolio.

Another attempt to modify the CAPM involves adjusting it for temporality. With temporal modeling, investors consider the consequences of decisions over multiple periods, instead of over the next period only, as the CAPM assumes. The resulting Consumption Capital Asset Pricing Model (CCAPM) is much more complex than its non-temporal counterpart. It has been shown to work successfully in situations where the normal CAPM has failed, most notably for forward exchange rates and for futures markets. Many other adaptations of the CAPM are in use. It is a validation of the widespread applicability of the CAPM that so many individuals have improved, transformed, or modified it to fit specific situations.

APPLYING THE CAPM

Despite limitations, the Capital Asset Pricing Model remains the best illustration of long-term tradeoffs between risk and return in the financial markets. Although very few investors actually use the CAPM without modification, its principles are very valuable, and may function as a sufficient guide for the average long-term investor.

These principles may be stated as:

1. Diversify—there is no compensation for unsystematic risk.
2. Hold long term—do not worry about timing when to get in or out of the market.
3. To earn a higher return, take on more systematic risk. The more stocks one holds that are sensitive to the business cycle the more average return the portfolio will receive. For shorter term, or more sophisticated investing, other models have been developed. However, unless the model is based on market inefficiencies, or obtaining superior information, it will still have the CAPM basic tenets at its center.