INDEX/INDEXES
Various kinds of indexes or index numbers are used by the scientific and academic communities, and the popular media. In fact, some indexes are so commonly used that one does not even recognize that they are index numbers, not absolute values of the variable or the item of interest. Changes in stock prices associated with several stock markets, for example, are quoted in terms of index numbers. Thus, when the media reports that the Dow fell by 200 points on a particular day, the reference is to the fall in the value of the index representing 30 industrial stocks included in the Dow Jones Industrial Average index, sometimes called the Dow 30. Suppose that the Dow Jones Industrial Average was at the 8,000 mark before it fell by 200 points. This implies that the average price of the 30 stocks included in the Dow index fell by 2.5 percent in one day ([200/8,000] * 100 = 2.5 percent). In order to understand index numbers, it is useful to have some idea of the methods of constructing indexes, and to be able to relate these methods to some common examples of index numbers.
THE WIDESPREAD USE OF INDEXES IN
BUSINESS AND ECONOMICS
A wide variety of sources generate the various indexes in the fields of business and economics. Many government agencies in the United States regularly produce information in index number form on a variety of variables. The Bureau of Labor Statistics under the U.S. Department of Labor reports data on various price indexes that are used to measure the inflation rate in the economy. The U.S. Department of Commerce also reports economic data on a regular basis. In addition to government sources, economic data are also reported (many of them in index number form) by private sources and by partisan and nonpartisan research organizations. Most business-related indexes can be categorized within two broad categories—those associated with the financial markets and those that describe the state of the economy.
INDEXES ASSOCIATED WITH THE FINANCIAL MARKETS.
There are many indexes associated with financial markets. These indexes measure different attributes of the financial markets at various degrees of depth and rigor. The majority of them track two major components of the financial markets: stock markets and bond markets.
Several index numbers measure the changes in stock prices at different levels of aggregation (that is, with respect to the number of stocks included in an index). The Dow Jones Industrial Average (DJIA), an index of 30 industrial stocks, is one of the most commonly followed stock price indexes. The DJIA includes major U.S. industrial stocks (such as CocaCola, IBM, General Motors, du Pont, Eastman Kodak, Disney, Sears, Goodyear, Merck, and AT&T) listed on the New York Stock Exchange (NYSE). There are also index numbers that represent stock price changes at a particular stock exchange or a stock-trading network. Thus, pertaining to the three trading mediums NYSE based in New York, the American Stock Exchange also based in New York (AMEX), and the computer-linked stock trading network of the National Securities Dealers Association (NASDAQ)—there are separate indexes called NYSE, AMEX, and NASDAQ, respectively. In addition to these so-called exchange-based indexes, there are several other stock price indexes that include an increasing number of stocks. For example, the S&P100 index, maintained by Standard & Poor's, measures stock price movements of 100 important stocks. Similarly, the S&P500 index measures the change in the aggregate price level of 500 selected stocks. The Wilshire 5000 index measures the change in the aggregate price level of the 5,000 stocks it monitors—a large number of stocks are included in this index to give a better picture of the overall stock market, rather than a narrow group of stocks.
By contrast, the bond market has far fewer indexes. The most widely used bond price index is the Lehman Brothers' bond price index; it measures changes in prices of long-term bonds included in the index. Changes in bond prices convey information regarding changes in interest rates. Thus, the bond price index is also closely watched by financial market participants.
INDEXES ASSOCIATED WITH THE ECONOMY.
Information and data on a large number of economic variables are regularly reported. Some of these data are reported in index number form. All price data in the economy are reported in index number form—as will be explained later, this is out of necessity, rather than choice. Three major price indexes are: Consumer Price Index, Producer Price Index, and Implicit Gross Domestic Product Price Deflator. Similarly, the Federal Reserve Bank computes the Index of Industrial Production on a monthly basis to gauge the pace of industrial production.
Other regularly reported indexes that describe the state of the economy (current or future) include: Index of Leading Indicators (LEI), which indicates the pace of economic activity in the economy in the near future; Consumer Confidence Index, which captures consumer sentiment and thus suggests consumers' willingness to spend; the Housing Affordability Index, which tracks the cost of being able to afford a home. Some indexes are not reported regularly, but occasionally crop up. For example, George Bush during his reelection campaign kept referring to the Misery Index, which captures the combined effects of inflation and unemployment.
THE NEED FOR AN INDEX.
Most economic variables are measured in absolute terms. For example, 12 million cars were produced in 1994 in the United States, or the gross output of goods and services in the United States was estimated at $8.7 trillion during 1998. It is not possible, however, to measure the price associated with a group of commodities in absolute terms; it can only be done so long as we refer to one commodity. We thus can say that the average price of a loaf of bread in the United States was $1.75 in 1998. But when dealing with a number of commodities together (as in the calculation of an individual's cost of living from year-to-year, one cannot simply compute the average price of all the goods and services bought in each year. Since most people buy a different set of commodities each year, the resulting averages would not be comparable. An index helps us out of this quandary. In the most basic terms, an index usually attaches weights to the prices of items in order to track the resulting collective price movement.
TYPES OF INDEX MEASUREMENTS
All indexes in the business and economics fields can be broadly placed in two categories: price indexes and quantity indexes. Price indexes measure changes in prices of a set of commodities, while quantity indexes measure changes in quantities of a set of commodities. Most common index numbers are price indexes, such as the Dow Jones Industrial Average and the Consumer Price Index.
CONSTRUCTION OF AGGREGATE PRICE
INDEXES
In its simplest form, a price index may be used to monitor changes in the price of one commodity over time—the price index shows how the current price of a given commodity compares with its price in a chosen base year (and in any other year in the past). Consider the example shown below from Statistics for Business and Economics, in which the price per gallon of unleaded gasoline is given for a nine-year period from 1982 to 1990:
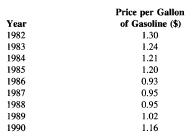
| Year | Price per Gallon of Gasoline ($) |
| 1982 | 1.30 |
| 1983 | 1.24 |
| 1984 | 1.21 |
| 1985 | 1.20 |
| 1986 | 0.93 |
| 1987 | 0.95 |
| 1988 | 0.95 |
| 1989 | 1.02 |
| 1990 | 1.16 |
To understand the changes in the gasoline price over the nine-year period, simple index numbers, called price relatives, are calculated. In this example, 1982 is considered the base period from which the price relatives will be calculated. A price relative for any particular year is then the price in that period divided by the base period price times 100. Thus, for 1982, the price relative is 100 ([1.30/1.30] * 100 = 100). For year 1983, the price relative is equal to 95 ([1.24/1.30] * 100 = 95). Thus, using simple price relatives, a series of price indexes for unleaded gasoline can be calculated as shown in the next table.
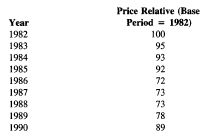
| Year | Price Relative (Base Period = 1982) |
| 1982 | 100 |
| 1983 | 95 |
| 1984 | 93 |
| 1985 | 92 |
| 1986 | 72 |
| 1987 | 73 |
| 1988 | 73 |
| 1989 | 78 |
| 1990 | 89 |
From this series of indexes, meaningful information about changes in the price of unleaded gasoline can be obtained. For example, between 1986 and 1990, the price relative for unleaded gasoline increased from 72 to 89. This suggests that gasoline prices increased by roughly 23.6 percent ([89-72]/ 72) * 100 = 23.6) during that period. Similarly, one can examine year-to-year changes in the price of gasoline, as well as compute price changes between any two years (or periods), using such a price relative series. Price relatives are very helpful in understanding changing economic and business conditions over time. They also form the basis for understanding the idea of index numbers.
AGGREGATE PRICE INDEXES.
Price relatives can only be used for individual items. In the real world, we are often concerned with the price change for a group of items taken together. For example, the DJIA uses a group of stocks to indicate the change in the average price of those stocks. Similarly, if we want an index that measures changes in the overall cost of living over time, we have to use a group of commodities (e.g., goods and services—food, clothing, medical care, etc.) that are bought by the individuals whose cost of living is being measured. In these instances, an aggregate price index is computed for the specific purpose of measuring the combined change in the prices of a group of items.
To illustrate the development of an aggregate price index for a group of items, one can consider the example of tracking changes in normal automotive operating expenses. For the sake of simplicity, only four items—gasoline, oil, tire, and insurance expenses—are included in the this example from Statistics for Business and Economics. Table I shows expense data in these categories for two years (1982 and 1996).
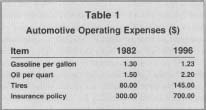
Automotive Operating
Expenses ($)
| Item | 1982 | 1996 |
| Gasoline per gallon | 1.30 | 1.23 |
| Oil per quart | 1.50 | 2.20 |
| Tires | 80.00 | 145.00 |
| Insurance policy | 300.00 | 700.00 |
Using 1982 as the base, an aggregate price index for automotive operative expenses can be calculated that will measure the change in operating expenses between 1982 and 1996. The simplest way of calculating an aggregate price index is to calculate an unweighted aggregate index. An unweighted aggregate index is found by simply summing the unit prices in the period of interest and then dividing the resulting amount by the sum of the unit prices in the base period. The ratio of the two sums is also multiplied by 100, a tradition followed in index number construction. Since in the present example 1996 expenses are being compared with the 1982 base, the unweighted price index for 1990 is equal to 249 ({[1.23 + 2.20 + 145.00 + 700.00]/[1.30 + 1.50 + 80.00 + 300.00]) * 100 = 222). Based on the calculated unweighted price index number for 1996, the price of normal automotive operating expenses increased by 122 percent between 1982 and 1996.
It can easily be seen that the unweighted aggregate index attaches the same weights to large per-unit price items in the group (such as insurance policy) and small per-unit price items (such as a gallon of gasoline). As a consequence, an unweighted aggregate price index is heavily influenced by items that have high per-unit price. This will be the case even if a large per-unit price item does not play a big role when one looks at the overall picture. In the present example, automotive operative expenses are too heavily influenced by price changes in tires and insurance coverage. It is because of the sensitivity of an unweighted aggregate price index to high-priced items that this measure of index is seldom used. A weighted aggregate price index coffects for the distortions caused by the unweighted aggregate price index.
WEIGHTED AGGREGATE PRICE INDEX.
The weighted aggregate price index improves on its unweighted counterpart by assigning a weight to each item in the group, in accordance with its importance in the overall group. In most instances, quantities of items used are employed as weights, as the quantity of usage provides the best indication of its importance in the group. To illustrate the construction of the weighted aggregate price index for the normal automotive operating expenses example, Table 2 provides data on annual usage of the four expense items. The weights provided are based on the assumption that a typical owner of a midsize automobile drives approximately 15,000 miles per year.

Annual Usage Information
| Item | Quantity Weights |
| Gasoline per gallon | 1000 |
| Oil per quart | 15 |
| Tires | 2 |
| Insurance policy | 1 |
The weighted aggregate price index is calculated in the same manner as unweighted aggregate price index, except that the unit price of a product is multiplied by its appropriate weight before the unit prices are summed up. The weighted aggregate price index for 1990 for the automotive expenses example is thus equal to 127 (f[(1.23 * 1000) + (2.20 * 15) + (145.00 * 2) + (700.00* 1)]/[(1.30* 1000) + (1.50* 15) + (80.00 * 2) + (300.00 * I)]} * 100 = 126). Based on this value, the price of automotive operating expenses increased by 26 percent between 1982 and 1996.
One can easily see that a weighted aggregate price index can yield a vastly different result than one that is unweighted. In the example, a 122-percent unweighted increase became a 26-percent weighted increase. The weighted aggregate price index provides a more accurate estimate of the magnitude of the price change for the group as a whole. While gasoline cost only $1.23 per gallon in 1996, a typical automotive operation involved 1,000 gallons of gasoline, resulting in a total expenditure of $1,230 on gasoline—much more than the $700 spent on automotive insurance. While the unweighted aggregate price index does not capture this effect, the weighted one does. As a general rule, quantities of usage are widely used as weights in constructing weighted aggregate price indexes for groups of items.
IMPORTANT ECONOMY-WIDE PRICE
INDEXES
Price indexes are used to measure the rate of inflation in the economy. There are three key price indexes that are routinely calculated and reported to the public by government sources in the United States. These three measures differ with respect to the number of items they take into account.
The inflation rate is derived by calculating the rate of change in a price index. The number of items included in a price index vary depending on the objective of the index. Usually three kinds of price indexes are periodically reported by government sources. They all have particular advantages and uses. The first index is called the consumer price index (CPI), which measures the average retail prices paid by consumers for goods and services bought by them. Several thousand products, grouped into 207 sets of items, are included in this index. These items are selected on the basis of their inclusion in the budget of a consumer (household). Each of the product prices is assigned a weight based on the importance of the item in the household budget. As a result, the CPI reflects the changes in the cost of living of a typical urban household. The CPI is considered the most relevant inflation measure from the point of view of the consumers, as it measures the prices of goods and services that are part of household budgets. Nevertheless, the CPI does not precisely measure the changes in the cost of living for every consumer because of differences in consumption patterns.
A second price index used to measure the inflation rate is called the producer price index (PPI). It is a much broader measure than the CPI. The PPI measures the wholesale prices of approximately 3,000 items. The items included in this index are those that are typically used by producers (manufacturers and businesses) and thus contain many raw materials and semi-finished goods. A change in the PPI reflects a change in the cost of production, incurred by producers. Since producers may pass a part or all of the increase in the cost of production to consumers, movements in the PPI indicate future movements in the CPI. The PPI can thus forewarn consumers of coming increases in the cost of living.
The implicit price deflator is the third measure of inflation. This index measures the prices of all goods and services included in the calculation of the current output of goods and services in the economy, known as gross domestic product (GDP). The implicit price deflator is the broadest measure of the price level. This index includes prices of fighter bombers purchased by the U.S. Department of Defense as well as paper clips used in offices. Thus, the implicit price deflator is a measure of the overall or aggregate price level for the economy. Movements in this index reflect the inflationary tendency of the overall economy.
The three measures of the inflation rate are most likely to move in the same direction, though not to the same extent. Differences can arise due to the differing number of goods and services included for the purpose of compiling the three indexes.
CALCULATIONS OF THE CONSUMER
PRICE INDEX AND THE INFLATION RATE
The construction of the consumer price index employs an index number technique, in which a fixed basket of commodities (a collection of goods and services considered relevant to the index) is valued using prices at different points of time. First, a point of reference or base is selected. Normally, a particular year is selected as the base. Currently, however, the 1982-84 period is used as the base in construction of the CPI in the United States. So, the average price of a commodity over the three-year period is used as the base price for the commodity for comparing to other periods. The price of each item in the basket of commodities selected is attached a weight in accordance with its importance in the budget of a typical urban family. In other words, the government must first identify the goods and services that are used by a typical urban consumer. Then, it must assign a weight to each of the items in the fixed basket—the basket thus contains a collection of goods and services in quantities that, presumably, a representative consumer consumes. Next, the government evaluates the fixed basket of commodities using prices at successive points and compares its costs (or values) with the cost to buy the same basket in the base year or period. This process generates a series of price ratios, which are usually multiplied by 100 for convenience. Thus, the price index is 100 in the base year or period, which the price index for other points of time reflect movements in the price level, which can be used to calculate the inflation rate between any two points.
With 1982-84 as the base, the consumer price index stood at 161.3 at the end of 1997, and at 163.9 at the end of 1998. The latter two values of the CPI imply that the cost of the fixed basket of commodities, compared to the base, had gone up by 61.3 percent by the end of 1997, and by 63.9 percent by the end of 1998. They also imply that the inflation rate during 1998 was roughly 1.6 percent on an annual basis (inflation rate = {(163.9 - 161.3)/161.3} * 100).
ITEMS INCLUDED IN THE CONSUMER PRICE INDEX.
The consumer price index is calculated by the U.S. Bureau of Labor Statistics (BLS), and it is published on a monthly basis. The broad categories of items that are included in construction of the CPI are: food and beverages, housing, apparel and upkeep, transportation, medical care, entertainment, and other goods and services. In reality, however, the CPI is based on several thousand products that are grouped into 207 sets of items. BLS employees visit thousands of stores in 85 geographical areas every month and collect more than 100,000 prices. Then, the average prices of related items, say, poultry and honey, are combined to yield group indexes—in this particular case, food and beverages. Next, the group indexes are combined to yield the overall price index called the "all-items CPI."
USEFULNESS OF THE CONSUMER PRICE INDEX.
The consumer price index is widely used, both in the private and public sectors. The CPI is most commonly used in calculating the inflation rate for general purposes. The movement in the consumer price index reflects the changes in the cost of living for urban consumers. Labor unions often use the CPI in bargaining for wage increases. Also, most government pensions, including the level of Social Security benefits, are indexed to the CPI.
CALCULATIONS OF THE PRODUCER
PRICE INDEX AND THE INFLATION RATE
The producer price index is also published by the U.S. Bureau of Labor Statistics (BLS) on a monthly basis. For the PPI, the BLS collects prices on more than 3,000 commodities that are purchased by businesses, not directly by consumers. In a simplified form, the producer price index can be thought of as having the following broad categories: (1) finished goods; (2) intermediate materials, supplies, and components; and (3) crude materials for further processing. Each of these broad categories is further subdivided in smaller groups. For example, the finished goods category consists of foods, energy, and finished goods excluding food and energy (the last subcategory includes capital equipment).
The producer price index uses an index number construction methodology similar to the consumer price index. While in case of the CPI the price data are directly collected by the BLS workers, the actual prices for the PPI are obtained from questionnaires mailed to thousands of firms that sell the products included in the PPI.
Currently, 1982 is used as the base for the producer price index series. The interpretation of the PPI series is similar to the CPI series—the PPI can also be used to calculate the inflation rate.
USEFULNESS OF THE PRODUCER PRICE INDEX.
One should recognize that the producer price index serves as an index relevant to the producers' cost. In other words, the PPI reflects what is happening to the cost of production. If the cost of production is rising, however, producers may also increase the prices at which they sell. This, in turn, is likely to increase the retail prices that consumers pay in stores across the nation. The PPI, thus, has an important information function—it forewarns coming changes in the consumer price index.
CALCULATIONS OF THE IMPLICIT PRICE
DEFLATOR AND THE INFLATION RATE
The implicit price deflator is arrived at in an indirect—or implicit—manner. Calculation of the consumer price index and the producer price index are explicit or direct; indexes are calculated from price data on the items included. The implicit price deflator, on the other hand, is inferred indirectly from the estimates of gross domestic product in nominal terms (in current dollars) and in real terms (when the nominal value of the GDP is adjusted for inflation by reevaluating it in prices that prevailed during a chosen base year).
Currently, 1992 is being used as the base year to calculate the real value of gross domestic product in the United States. Thus, the 1998 U.S. output of goods and services is first evaluated at prices prevailing in 1998. Once this is done, 1998 output of goods and services is also evaluated at prices that prevailed in 1992 (thus, the terms gross domestic product in 1992 dollars or constant dollars). One can easily see how the ratio of gross domestic product in 1998 prices and gross domestic product in 1992 prices would yield a measure of the extent of the rise in price level between 1992 and 1998. According to the federal government statistics, this ratio is estimated at 1.1307, or 113.07 when multiplied by 100 (as is customarily done to determine the extent of price increase more conveniently). The value of implicit price deflator of 113.07 implies that the price level increased by 13.07 percent over the 1992-1998 period (note that the base year, currently 1992, value of implicit price deflator is equal to 100).
This method of expressing nominal or current gross domestic product into its value in 1992 prices is routinely done every year (of course, sometimes the base year itself, may be changed to a later year to keep the data series closer to the current period). Thus, we have 1997, 1996, 1995 (and so on) gross domestic products expressed in 1992 prices. This helps to calculate the inflation rate between subsequent years. For example, the implicit price deflator stood at 112.08 at the end of 1997. Given that the deflator was at 113.07 at the end of 1998, we arrive at the annual inflation rate of roughly 0.88 percent during 1998 (1998 inflation rate = [(113.07 - 112.08) / 112.08] * 100).
Since the implicit price deflator is derived from the nominal and real values of the gross domestic product (GDP), it is also called implicit GDP price deflator. One should also notice that the term deflator is not used in consumer and producer price indexes. This is because, if one knows the implicit price deflator for 1998, and the 1998 gross domestic product in current prices, one could arrive at the gross domestic product in 1992 prices by deflating the 1998 gross domestic product in current prices by the deflator for 1998 (expressed in plain ratio form, rather than the one multiplied by 100). Despite the use of term deflator, one should not lose sight of the fact the implicit price deflator is essentially a price index.
USEFULNESS OF THE IMPLICIT GDP PRICE DEFLATOR.
As noted, the implicit price index is the broadest measure of price level. Although changes in it reflect the inflation pressure underlying the whole economy, since this index is all-inclusive, it may not be directly useful to ordinary households and even businesses. The CPI and PPI are more relevant to these units.
USEFULNESS OF THE THREE PRICE
INDEXES
As mentioned earlier, all three price indexes can be used to calculate the inflation rate. There are, however, two important differences among these indexes. First, the consumer and producer price indexes are published every month, whereas the implicit GDP price deflator figures are reported on a quarterly basis. Thus, more frequent users of inflation data would be inclined to use the CPI or the PPI. Second, coverage of the three indexes varies dramatically. Thus, one of these price index series can be more suitable than the other two in particular cases. To measure the cost of living of an urban consumer, for example, the CPI will be overwhelmingly preferred to the PPI and the implicit GDP price deflator. Nevertheless, one must be aware that even the CPI is an average price measure that is based on certain weights. While the CPI may reflect the cost of living changes of consumers on average, it cannot precisely reflect changes in the actual cost of living of a particular consumer; his or her consumption pattern may be quite different from that assumed in assigning weights to the fixed basket of commodities. One thus needs to interpret the price index numbers carefully.
Despite the slight caution one must exercise in interpreting the price indexes, a good understanding of the inflation rate, that all three price indexes are designed to yield, is important for every individual and household. Most economies face positive rates of inflation year after year. If the inflation rate is positive and an individual's income remains constant, his or her real standard of living will fall as the individual's income will be worth less and less in successive periods. Let us assume that a household earns $50,000 per year and the income remains fixed at this level in the future. If the inflation rate persists at 10 percent per year, the purchasing power of the household income will also keep declining at the rate of 10 percent per year. At the end of the five-year period, prices will be one and a half times greater. This will lead to the household being able to buy only two-thirds of the goods and services it was able to buy at the beginning of the period.
An understanding of inflation is also crucial in making plans to save for retirement, children's education, or even a luxury purchase. One must use an appropriate price index in calculating the funds required for a given purpose. The consumer price index is a good guide for retirement purposes. If one is saving to buy a boat, however, even the CPI may not produce a good result—the individual may want to know the way boat prices are increasing. Nevertheless, an understanding of the price indexes prepares an individual to explore such scenarios further.
QUANTITY INDEXES
Another use of index numbers, in addition to measuring changes in prices, is to measure changes in quantity levels over time. This type of index is called a quantity index. In discussing price indexes, emphasis was placed on the weighted aggregate price index as an index number methodology of choice. A set of weights are also used to compute quantity indexes. The weighted aggregate quantity index is computed essentially in a manner similar to that for a weighted aggregate price index. As a weighted aggregate quantity index seeks to measure changes in quantities, it obviously cannot use quantity usage as weights. Analogous to weighted aggregate price indexes, the weighted aggregate quantity index uses fixed price weights—that is, quantities are weighted by associated prices. Except for the weights used, construction of price and quantity indexes employs the same index number methodology.
A well-known example of the quantity indexes is the Index of Industrial Production (IIP), developed by the central bank of the United States (the Federal Reserve Bank). This index is designed to measure changes in production levels for a variety of items in the manufacturing, mining, and utilities sectors. In general terms, the IIP Production is used to monitor the pace of economic activity in the industrial sector, considered to be the core sector of the U.S. economy. This index is reported on a monthly basis and it uses 1992 as the base year. Since the GDP, a comprehensive measure of economic activity in the United States, is reported only on a quarterly basis, the IIP provides more frequent measures of changes in production levels in the economy.
SEE ALSO : Consumer Price Index (CPI) ; Price Indexes
[ Anandi P. Sahu , Ph.D. ]
FURTHER READING:
Anderson, David R., Dennis J. Sweeney, and Thomas A. Williams. Statistics for Business and Economics. 7th ed. St. Paul, MN: West Publishing Company, 1999.
Froyen, Richard T. Macroeconomics: Theories and Policies. 6th ed. Upper Saddle River, NJ: Prentice Hall, 1998.
Gordon, Robert J. Macroeconomics. 7th ed. Reading, PA: Addison-Wesley, 1998.
Sommers, Albert T. The U.S. Economy Demystified. Lexington, MA: Lexington Books, 1985.