PORTFOLIO MANAGEMENT THEORY

The theory of portfolio management describes the resulting risk and return of a combination of individual assets. A primary objective of the theory is to identify asset combinations that are efficient. Here, efficiency means the highest expected rate of return on an investment for a specific level of risk. The primary starting point for portfolio theory requires an assumption that investors are risk averse. This simply means that they will not consider a portfolio with more risk unless it is accompanied by a higher expected rate of return.
Modern portfolio theory was largely defined by the work of Harry Markowitz (1927-) in a series of articles published in the late 1950s. This theory was extended and refined by William Sharpe (1934-), John Lintner (1916 1983), James Tobin (1918-), and others in the subsequent decades. Portfolio theory integrates the process of efficient portfolio formation to the pricing of individual assets. It explains that some sources of risk associated with individual assets can be eliminated, or diversified away, by holding a proper combination of assets.
To begin the development of a theory of effective portfolio management, consider the following set of four individual securities as shown in Figure 1.

Risk and Return for Individual Securities
If investors are restricted to holding a single security, and since they prefer higher returns to lower returns, they will prefer B to C. Likewise, investors prefer less risk to more risk, so they will prefer B to D and A to C. Thus no rational, risk-averse investor will hold C or D. But what about the remaining portfolios A and B? The decision here is less clear. Neither portfolio is dominated by any of the others. Thus, investors must decide whether the additional expected return of B is adequate compensation for the additional risk it also exhibits. If these are the only four alternatives, then A and B are efficient portfolios since they exhibit the highest return for a given risk level. Rational investors, however, may now disagree on which of the two portfolios to select.
Now, suppose that investors can apportion their investment into A, B, or some of each. The expected return of this new set of two security portfolios will be a simple weighted average of the expected returns of the individual elements. For example, if the expected return on A were 12 percent and the expected return on B were 20 percent, then a portfolio with an equal proportion of each would be expected to return 16 percent. If the proportion of B was increased, the expected return would rise. Conversely, it would decline if the proportion of A was enhanced. Determining the risk inherent in these two security portfolios is somewhat more complex. There is a risk component contributed from A, another from B, and a third that results form the comovement of A and B. Statistically, this third component is referred to as covariance, or correlation. This comovement term can be strong or weak. It can also positive, indicating that the returns from A and B tend to move in the same direction, or negative, indicating that A and B tend to move in opposite directions.
Although the comovement component makes risk analysis of portfolios more complicated, it also represents the source of risk diversification and provides superior investment alternatives for many investors than can be attained by holding A or B in isolation. This is the insight that Markowitz was able to formalize. For example, if the returns generated by A and B exhibit moderate and positive comovement (or correlation), then portfolios of A and B would have expected return and risk characteristics as illustrated in Figure 2.
The set of combinations of A and B illustrated in Figure 2 are referred to as the opportunity set. Note that some portfolios that are attainable would not be desirable to a savvy risk-averse investor. For example, no investor will hold a 100 percent A portfolio since there is a combination containing some B that has the same level of risk and greater expected return. In fact, this is true for all portfolios represented on the lower half of the curve. The efficient frontier is the name given to the subset of the opportunity set containing
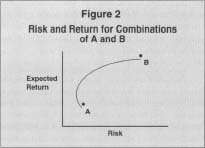
Risk and Return for Combinations of A and B
Next, consider this same problem with more than two securities to consider. The expected return of any combination of any number of securities remains a weighted average of the expected returns of the individual components, but the risk calculation must now contain a comovement, or correlation term for each unique pair of securities under consideration. Even though this requires a large amount of calculation, it can be accomplished. The resulting opportunity set is now represented by the area behind the curve in Figure 3. The efficient frontier of combinations of these risky individual securities, however, are the portfolios represented along the upper edge of the curve itself.
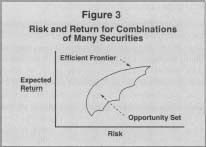
Risk and Return for Combinations of Many Securities
Which of these efficient portfolios is best for an individual investor? It depends upon that investor's personal level of risk aversion. Investors with high risk tolerance will choose portfolios to the right and those with low levels of risk tolerance will choose portfolios toward the left. Regardless, all investors should consider only those portfolios that are members of the efficient frontier.
A further refinement in this analysis can be obtained if there is a risk-free asset to consider as well. A truly riskless security will have a certain return and will therefore have no correlation with the uncertain returns from other individual securities or portfolios. Combinations of the risk-free security and a risky portfolio, Y, lie on the lowest broken line in Figure 4.
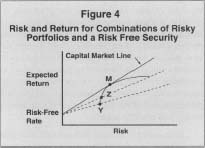
Risk and Return for Combinations of Risky Portfolis and a Risk Free Secruity
Note that investors can now achieve lower risk positions than are possible by holding only combinations of risky securities. Investors choosing to place a portion of their wealth in Y and the rest in the risk-free security will attain a portfolio that appears on the straight-line segment connecting those two components. If it were possible to borrow at the risk-free rate, investors could actually attain higher returns (for higher risk). These portfolios are represented by points on the broken line to the right of Y. These combinations, however, would not be efficient since there are pure combinations of risky securities that offer higher returns at similar risk levels.
Since portfolio Y is not unique, consider a different combination of risky assets, Z. Combinations of Z and the risk-free security lie upon a line connecting these two points. Clearly, any investors, regardless of their attitude toward risk, would prefer to select among combinations of Z and the risk-free security than combinations of Y and the risk-free security since there are higher expected returns at all risk levels. Portfolio Z, however, is not unique either and there are other risky portfolios that would provide superior returns when combined with the risk-free security. This process can be repeated until a particular portfolio M is identified. The line defining the expected returns and risk of combinations of M and the risk-free security is tangent to the former efficient frontier. Risky portfolios with higher expected return than M would not offer superior alternatives in conjunction with the risk-free security. Therefore, M is a unique combination. Investors who prefer a level of risk below that of M will hold a combination of M and the risk-free security. Their portfolios would plot between these two points on the graph. Investors who desire a risk level in excess of M can borrow at the risk-free rate and invest more than 100 percent of their original wealth in M. This will allow them to position themselves at points on the line above and to the right of M. In this scenario, the new efficient frontier is the solid line in Figure 4.
While M is unique in geometric terms, it is also unique in economic terms. Once this portfolio is identified, every investor, regardless of risk preferences, should choose combinations of M and the risk-free security. All investors should be allocating their wealth between M and the risk-free security. This has several important implications. First, all risky assets must be included in M. If not, then the price of excluded assets will quickly fall to a point where its rate of return will suggest membership in M. Since all assets are included in M, it is commonly referred to as the market portfolio.
The line passing through M is called the capital market line (CML). The
slope of this line represents the price of additional units of expected
return per unit of additional risk. Once the CML is defined, the next step
is to determine the implications of portfolio M in deriving proper
required returns for the individual securities it contains. One model that
does this is the
capital asset pricing model
(CAPM). The CAPM indicates that the proper expected return for an
individual security is related to its risk relative to the overall risk
level of M. This relationship can be defined in the following equation.
The return a security (or portfolio) is expected to generate in excess of the risk-free rate is called a risk premium. The expected return for a security must include a risk premium that is some multiple of the risk premium for the entire market. In this equation, 0 (or beta) is the risk of the individual security relative to the overall risk level of the market. A security with above-average risk would have a β in excess of 1 and a below-average risk security would have a β below 1. Since the aggregate of individual securities is the market itself, β for portfolio M is exactly 1.
Recall that the main benefit of forming portfolios is the potential to create combinations with lower risk and possibly higher expected returns than can be obtained from individual securities. Now consider the risk associated with an individual security as the sum of two parts. One part is represented by risk factors that are truly unique to the specific security. The other part is represented by risk factors that are essentially common with all other securities. For example, the potential for a key employee to leave the firm unexpectedly or the possibility of discovering gold under corporate headquarters are unique risk factors that are not shared with other firms. On the other hand, risk factors concerning the potential for unexpected and rapid growth in the national (or international) economy or the enactment of new legislation that affects the operating costs for all firms represent examples of common risk factors. While portfolio formation reduces the influence of unique risks associated with individual securities, it cannot eliminate exposure to common risk factors. Stated differently, properly constructed portfolios allow for diversification of unsystematic (unique) risk, but not for systematic (market) risk.
Using this latest interpretation, β represents the level of systematic risk of an individual security. Since investors have the potential to eliminate unsystematic risk from their portfolios, the return they expect should only include compensation for the systematic risk component. This is the underlying message of the CAPM.
There are other theories that attempt to explain how individual securities
are priced. One prominent one is
arbitrage
pricing theory (APT). While CAPM essentially uses the market's
risk premium as the sole determinant of a security's return, APT
allows for multiple systematic risk factors. A simple representation of
the APT model is provided below.
Systematic risk is now measured with respect to a variety of factors, not just market returns. While three factors are listed here, there may be more or fewer. Furthermore, the factors themselves are not specified by the theory. This means that any application of the theory requires the user to commit to a specific set of factors that can be justified both economically and statistically.
This is a good place to review the implications of portfolio theory. First, investors are risk averse and will accept more risk only if there is the expectation of higher return as well. This suggests that they will seek and hold only efficient combinations of securities. These efficient combinations have exploited the role of comovement among the individual securities to eliminate all diversifiable, or unsystematic risk. The returns expected from individual securities will therefore include no premium for diversifiable risk since it can be eliminated. The only source of risk requiring compensation is systematic, or market, risk.
It is also worth noting that if a risk-free asset is also available, there is a single risky portfolio (referred to as M, or the market portfolio) that is optimal for all investors. Investors will seek their desired level of risk exposure by selecting the proper proportions of the risky portfolio, M, and the risk-free asset.
As a practical matter, it is difficult to identify the true market portfolio since it, by definition, must contain proportions of all assets that have value. This means that investors and portfolio managers must create proxies for the market portfolio from some subset of all possible investments. Even if this proxy can be identified and created, the efficient frontier moves around as expected return and risk of the individual securities, and correlation among these elements, change over time. Moreover, it is impossible to estimate future risk and return without error. This leads some practitioners to view the efficient frontier as "fuzzy."
Three alternative approaches to portfolio management arise from these considerations. Many investors default to a passive portfolio strategy. A passive strategy requires the investor to buy and hold some replica of the market portfolio and accept an expected return equal to the market. For example, an investor may choose to hold a portfolio of stocks that is identical to the Standard & Poor's 500 or some other broad market index. This becomes the risky component of the portfolio and is combined with a proportion of a risk-free security (e.g., U.S. Treasury bills) to achieve the desired risk level. Underlying this strategy is the assumption that markets are reasonably efficient and that any attempt to improve the rate of return from risky securities is not likely to succeed. The broad market index is likely to reside within the "fuzzy" domain of the efficient frontier.
Active portfolio management strategies attempt to "beat the market" by identifying "mispriced" securities and forming efficient portfolios from those securities. This strategy clearly requires more effort from the investor. If such securities can be identified and the market eventually prices them properly, the active portfolio will generate returns in excess of those provided by the market on a risk adjusted basis.
A third approach relies on intensive quantitative analysis of securities specified by an investor. An optimization algorithm can provide an efficient allocation of funds among a given set of alternatives. This approach can be applied to an existing passive or active strategy.
In summary, portfolio management theory assesses risk and return relationships for combinations of securities. While the expected return of a portfolio is the simple weighted average of the expected returns of its component securities, portfolio risk must also consider the correlation among the returns of individual securities. Since part of the price fluctuation of a security is unique, it does not relate to price fluctuations of other securities held. This allows the investor to diversify, or eliminate, a portion of each security's risk. With additional analysis, the subset of portfolios with the highest expected return for a given risk level can be identified. If a risk-free asset can also be purchased or sold, then there is a unique combination of risky securities that will allow all investors to achieve superior returns for a given risk level. The capital asset pricing model and other models use this result to infer the risk-return relationship for individual securities. Although there is imprecision when attempting to implement these theories, they provide a useful way to evaluate and improve a variety of investment strategies.
[ Paul Bolster ]
FURTHER READING:
Bodie, Zvi, Alex Kane, and Alan J. Marcus. Investments. 4th ed. Boston: Irwin/McGraw-Hill, 1999.
Grinold, Richard C., and Ronald N. Kahn. Active Portfolio Management. 2nd ed. New York: McGraw-Hill, 1999.
Markowitz, Harry. Portfolio Selection: Efficient Diversification of Investments. 2nded. Cambridge, MA: Basil Blackwell, 1991.
Michaud, Richard 0. Efficient Asset Management. Boston: Harvard Business School Press, 1998.
Comment about this article, ask questions, or add new information about this topic: