PRESENT VALUE

The present value (PV) of an amount to be received in the future is the discounted face value considering the length of time the receipt is deferred and the required rate of return (or appropriate discount rate under the circumstances). The notion of present value presumes that money has a time value—today 1 ;s dollar is worth more than the same dollar received at a future point in time—deriving from inflation, interest, and other considerations. This idea is used commonly when planning a capital budget.
This notion can be demonstrated by examining three common financial transactions:
- Money invested in bank certificates of deposit may earn interest at 5 percent. At that rate, $1,000 deposited on January 1 will accumulate $50 of interest by December 31, making the total available to the investor $1,050. Since this investor is willing to lend his money to the bank for 5 percent annual interest, that rate may be viewed as the required rate of return, or the discount rate. The $1,050 to be received on December 31 had a PV to that investor at January I of exactly $1,000 (1,050/(1 +.05)').
- Annuity contracts can be bought from insurance companies whereby a single payment is made to the insurance company in exchange for a defined series of annual (or monthly) payments made back to the buyer. In these cases the simple sum of the periodic repayments from the insurance company to the buyer exceed the original annuity purchase price, in absolute terms. However, when considering the deferred repayment and the implied rate of return on the money loaned, the amounts exactly equate, on a present value basis.
- Mortgage loans are basically the reverse of the above described annuity contract. Here, the individual borrows the money, promising to make scheduled repayments to the lender. Again, due to the differential timing of cash flows, and the fact that the bank requires interest to be paid on the borrowed funds, the PVs equate. That is, the PV of the sum of the future mortgage payments is exactly equal to the amount borrowed (which by definition is at the PV on the date of the loan).
CALCULATING PRESENT VALUE
The formula for calculating the present value of a series of future
receipts is:
where CF
1
to
CF
n
=
future receipts
i = the interest or discount rate appropriate for the stated period
n
= the number of periods over which future receipts occur
RATE OF RETURN.
The interest or discount rate used in PV calculations is a key element in determining the PV. This importance is emphasized when the future amounts occur over an extended period of time, due to the power of compounding. For example, the final payment on a 30-year loan at 7 percent interest would be worth approximately 13.1 percent of its face amount on a present value basis at the date of loan origin [1/(1 + .07) 30 ]. By contrast, the 30th payment on a loan with a 9 percent interest rate would be worth only 7.5 percent [1/(1 + .09) 30 ] of its face amount in present value terms at the origin. This simple example shows the power of compounding when time periods are long.
The discount rate used in a given circumstance must provide for compensation to the lender of funds for three elements of return:
- Inflation: just to keep even in terms of buying power, the return of money at a future date must be appended by the rate of general price inflation as measured by the Consumer Price Index (CPI). In other words, if a person lends an amount of money adequate to buy a loaf of bread at time t=0, he will require repayment at t = I of the original amount plus the fraction of that amount representing the CPI increase over the period. That way he will be able to buy the same loaf of bread at t = 1.
- Time value of money (TVM): beyond simply keeping even with inflation, the investor or lender has a basic preference for consumption sooner rather than later. The cost of compensating for this aspect of human nature has been found to be about 1 to 2 percent per year. That is, the real rate of return on risk-free assets has averaged about 1.5 percent.
- Risk: in addition to postponing the preferred immediate consumption and having to reimburse for inflation's erosion of buying power, many types of investment involve a risk of default. That is, the investor may never again see his funds, for example if the company goes bankrupt. Compensating for this element of required return can be considerably more expensive than the first two combined. For example, junk bonds may be paying interest at 12 percent, while anticipated inflation is only 4 percent and TVM is about 1.5 percent. This would mean that the risk premium component of the overall interest rate is 6.5 percent (12 percent—4 percent—1.5 percent).
NET PRESENT VALUE
An important extension of present value is net present value (NPV), which is simply the sum of present values for an investment's anticipated returns over time offset by its up-front costs. This is an important decision-making tool because an investment may appear lucrative in today's money, but once its returns are discounted it may reveal the investment would yield a net loss for the company compared to other options.
Imagine a company that has an opportunity to invest in a five-year joint venture with another firm beginning in 2002. The company would have to put up $100,000 at the start to fund its share, but the annual returns to the company are expected be $30,000 a year for five years. On the surface, it appears that the company would reap a 50 percent return on its investment, since $30,000 × 5 = $150,000.
Net present value paints a different scenario, however. Recall from the time value of money theory that $50,000 in five years is worth less than the same nominal figure today. There are also opportunity costs and capital acquisition costs to consider. What is the company losing by not using the $100,000 elsewhere? and how much does it cost the company to obtain new capital?
The latter question forms the basis for determining a minimum required rate of return on such an investment; if the returns on capital don't at least match the costs of obtaining it, the investment is losing money.
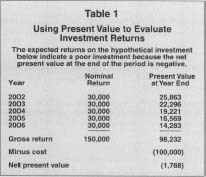
Using Present Value to Evaluate
Investment Returns
| The expected returns on the hypothetical investment below indicate a poor investment because the net present value at the end of the period is negative. | ||
| Year | Nominal Return | Present Value at Year End |
| 2002 | 30,000 | 25,863 |
| 2003 | 30,000 | 22,296 |
| 2004 | 30,000 | 19,221 |
| 2005 | 30,000 | 16,569 |
| 2006 | 30,000 | 14,283 |
| Gross return | 150,000 | 98,232 |
| Minus cost | (100,000) | |
| Net present value | (1,768) | |
With that in mind, suppose the company determines that its minimum rate of return is 16 percent given current interest rates, inflation, the risks associated with the investment, and so forth. Table I shows how the net present value of the venture would be computed. As the figures indicate, once the annual returns are discounted based on the company's capital costs and other factors, their present values as of 2002 would yield a negative NPV, a signal to management that the venture is probably not worthwhile. Not only would management expect a positive NPV, but if it has several options it would likely choose the one with the highest positive NPV.
SEE ALSO : Discounted Cash Flow
FURTHER READING:
Birrer, G. Eddy, and Jean L. Carrica. Present Value Applications for Accountants and Financial Planners. Westport, CT: Quorum Books, 1990.
Robison, Lindon J., and Pete J. Barry. Present Value Models and Investment Analysis. East Lansing, MI: Michigan State University Press, 1998.
Comment about this article, ask questions, or add new information about this topic: