TAGUCHI METHODS

There has been a great deal of controversy about Genichi Taguchi's methodology since it was first introduced in the United States. This controversy has lessened considerably in recent years due to modifications and extensions of his methodology. The main controversy, however, is still about Taguchi's statistical methods, not about his philosophical concepts concerning quality or robust design. Furthermore, it is generally accepted that Taguchi's philosophy has promoted, on a worldwide scale, the design of experiments for quality improvement upstream, or at the product and process design stage.
Taguchi's philosophy and methods support, and are consistent with, the Japanese quality control approach that asserts that higher quality generally results in lower cost. This is in contrast to the widely prevailing view in the United States that asserts that quality improvement is associated with higher cost. Furthermore, Taguchi's philosophy and methods support the Japanese approach to move quality improvement upstream. Taguchi's methods help design engineers build quality into products and processes. As George Box, Soren Bisgaard, and Conrad Fung observed: "Today the ultimate goal of quality improvement is to design quality into every product and process and to follow up at every stage from design to final manufacture and sale. An important element is the extensive and innovative use of statistically designed experiments."
TAGUCHI'S DEFINITION OF QUALITY
The old traditional definition of quality states quality is conformance to specifications. This definition was expanded by Joseph M. Juran (1904-) in 1974 and then by the American Society for Quality Control (ASQC) in 1983. Juran observed that "quality is fitness for use." The ASQC defined quality as" the totality of features and characteristics of a product or service that bear on its ability to satisfy given needs."
Taguchi presented another definition of quality. His definition stressed the losses associated with a product. Taguchi stated that "quality is the loss a product causes to society after being shipped, other than losses caused by its intrinsic functions." Taguchi asserted that losses in his definition "should be restricted to two categories: (1) loss caused by variability of function, and (2) loss caused by harmful side effects." Taguchi is saying that a product or service has good quality if it "performs its intended functions without variability, and causes little loss through harmful side effects, including the cost of using it."
It must be kept in mind here that "society" includes both the manufacturer and the customer. Loss associated with function variability includes, for example, energy and time (problem fixing), and money (replacement cost of parts). Losses associated with harmful side effects could be market shares for the manufacturer and/or the physical effects, such as of the drug thalidomide, for the consumer.
Consequently, a company should provide products and services such that possible losses to society are minimized, or, "the purpose of quality improvement … is to discover innovative ways of designing products and processes that will save society more than they cost in the long run." The concept of reliability is appropriate here. The next section will clearly show that Taguchi's loss function yields an operational definition of the term "loss to society" in his definition of quality.
TAGUCHI'S LOSS FUNCTION
We have seen that Taguchi's quality philosophy strongly emphasizes losses or costs. W. H. Moore asserted that this is an "enlightened approach" that embodies "three important premises: for every product quality characteristic there is a target value which results in the smallest loss; deviations from target value always results in increased loss to society; [and] loss should be measured in monetary units (dollars, pesos, francs, etc.)."
Figure I depicts Taguchi's typically loss function. The figure also contrasts Taguchi's function with the traditional view that states there are no losses if specifications are met.
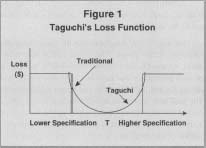
Taguchi's Loss Function
It can be seen that small deviations from the target value result in small
losses. These losses, however, increase in a nonlinear fashion as
deviations from the target value increase. The function shown above is a
simple quadratic equation that compares the measured value of a unit of
output
Y
to the target
T.:
where
L(Y)
is the expected loss associated with the specific value of
Y.
Essentially, this equation states that the loss is proportional to the square of the deviation of the measured value, Y, from the target value, T. This implies that any deviation from the target (based on customers' desires and needs) will diminish customer satisfaction. This is in contrast to the traditional definition of quality that states that quality is conformance to specifications. It should be recognized that the constant k can be determined if the value of L(Y) associated with some Y value are both known. Of course, under many circumstances a quadratic function is only an approximation.
Since Taguchi's loss function is presented in monetary terms, it
provides a common language for all the departments or components within a
company. Finally, the loss function can be used to define performance
measures of a quality characteristic of a product or service. This
property of Taguchi's loss function will be taken up in the next
section. But to anticipate the discussion of this property,
Taguchi's quadratic function can be converted to:
This can be accomplished by assuming Y has some probability distribution with mean, a and variance o.2 This second mathematical expression states that average or expected loss is due either to process variation or to being off target (called "bias"), or both.
TAGUCHI, ROBUST DESIGN, AND THE
DESIGN OF EXPERIMENTS
Taguchi asserted that the development of his methods of experimental design started in Japan about 1948. These methods were then refined over the next several decades. They were introduced in the United States around 1980. Although, Taguchi's approach was built on traditional concepts of design of experiments (DOE), such as factorial and fractional factorial designs and orthogonal arrays, he created and promoted some new DOE techniques such as signal-to-noise ratios, robust designs, and parameter and tolerance designs. Some experts in the field have shown that some of these techniques, especially signal-to-noise ratios, are not optimal under certain conditions. Nonetheless, Taguchi's ideas concerning robust design and the design of experiments will now be discussed.
DOE is a body of statistical techniques for the effective and efficient collection of data for a number of purposes. Two significant ones are the investigation of research hypotheses and the accurate determination of the relative effects of the many different factors that influence the quality of a product or process. DOE can be employed in both the product design phase and production phase.
A crucial component of quality is a product's ability to perform its tasks under a variety of conditions. Furthermore, the operating environmental conditions are usually beyond the control of the product designers, and, therefore robust designs are essential. Robust designs are based on the use of DOE techniques for finding product parameter settings (e.g., temperature settings or drill speeds), which enable products to be resilient to changes and variations in working environments.
It is generally recognized that Taguchi deserves much of the credit for introducing the statistical study of robust design. We have seen how Taguchi's loss function sets variation reduction as a primary goal for quality improvement. Taguchi's DOE techniques employ the loss function concept to investigate both product parameters and key environmental factors. His DOE techniques are part of his philosophy of achieving economical quality design.
To achieve economical product quality design, Taguchi proposed three phases: system design, parameter design, and tolerance design. In the first phase, system design, design engineers use their practical experience, along with scientific and engineering principles, to create a viably functional design. To elaborate, system design uses current technology, processes, materials, and engineering methods to define and construct a new "system." The system can be a new product or process, or an improved modification of an existing product or process.
The parameter design phase determines the optimal settings for the product or process parameters. These parameters have been identified during the system design phase. DOE methods are applied here to determine the optimal parameter settings. Taguchi constructed a limited number of experimental designs, from which U.S. engineers have found it easy to select and apply in their manufacturing environments.
The goal of the parameter design is to design a robust product or process, which, as a result of minimizing performance variation, minimizes manufacturing and product lifetime costs. Robust design means that the performance of the product or process is insensitive to noise factors such as variation in environmental conditions, machine wear, or product to-product variation due to raw material differences. Taguchi's DOE parameter design techniques are used to determine which controllable factors and which noise factors are the significant variables. The aim is to set the controllable factors at those levels that will result in a product or process being robust with respect to the noise factors.
In our previous discussion of Taguchi's loss function, two equations were discussed. It was observed that the second equation could be used to establish quality performance measures that permit the optimization of a given product's quality characteristic. In improving quality, both the average response of a quality and its variation are important. The second equation suggests that it may be advantageous to combine both the average response and variation into a single measure. And Taguchi did this with his signal-to-noise ratios (S/N). Consequently, Taguchi's approach is to select design parameter levels that will maximize the appropriate S/N ratio.
These S/N ratios can be used to get closer to a given target value (such as tensile strength or baked tile dimensions), or to reduce variation in the product's quality characteristic(s). For example, one S/N ratio corresponds to what Taguchi called "nominal is best." Such a ratio is selected when a specific target value, such as tensile strength, is the design goal.
For the "nominal is best" case, Taguchi recommended finding
an adjustment factor (some parameter setting) that will eliminate the bias
discussed in the second equation. Sometimes a factor can be found that
will control the average response without affecting the variance. If this
is the case, our second equation tells us that the expected loss becomes:
Consequently, the aim now is to reduce the variation. Therefore,
Taguchi's S/N ratio is:
where
S
2
is the sample's standard deviation.
In this formula, by minimizing S 2 , − 10 log 10 S 2 , is maximized. Recall that all of Taguchi's S/N ratios are to be maximized.
Finally, a few brief comments concerning the tolerance design phase. This phase establishes tolerances, or specification limits, for either the product or process parameters that have been identified as critical during the second phase, the parameter design phase. The goal here is to establish tolerances wide enough to reduce manufacturing costs, while at the same time assuring that the product or process characteristics are within certain bounds.
EXAMPLES AND CONCLUSIONS
As Thomas P. Ryan has stated, Taguchi at the very least, has focused "our attention on new objectives in achieving quality improvement. The statistical tools for accomplishing these objectives will likely continue to be developed." Quality management "gurus," such as W. Edwards Deming (1900-1993) and Kaoru Ishikawa (1915-), have stressed the importance of continuous quality improvement by concentrating on processes upstream. This is a fundamental break with the traditional practice of relying on inspection downstream. Taguchi emphasized the importance of DOE in improving the quality of the engineering design of products and processes. As previously mentioned, however," his methods are frequently statistically inefficient and cumbersome." Nonetheless, Taguchi's design of experiments have been widely applied and theoretically refined and extended. Two application cases and one refinement example will now be discussed.
K. N. Anand, in an article in Quality Engineering, discussed a welding problem. Welding was performed to repair cracks and blown holes on the cast-iron housing of an assembled electrical machine. Customers wanted a defect-free quality weld, however the welding process had resulted in a fairly high percentage of welding defects. Management and welders identified five variables and two interactions that were considered the key factors in improving quality. A Taguchi orthogonal design was performed resulting in the identification of two highly significant interactions and a defect-free welding process.
The second application, presented by M. W. Sonius and B. W. Tew in a Quality Engineering article, involved reducing stress components in the connection between a composite component and a metallic end fitting for a composite structure. Bonding, pinning, or riveting the fitting in place traditionally made the connections. Nine significant variables that could affect the performance of the entrapped fiber connections were identified and a Taguchi experimental design was performed. The experiment identified two of the nine factors and their respective optimal settings. Therefore, stress levels were significantly reduced.
The theoretical refinement example involves Taguchi robust designs. We have seen where such a design can result in products and processes that are insensitive to noise factors. Using Taguchi's quadratic loss function, however, may provide a poor approximation of true loss and suboptimal product or process quality. John F. Kros and Christina M. Mastrangelo established relationships between nonquadratic loss functions and Taguchi's signal-to-noise ratios. Applying these relationships in an experimental design can change the recommended selection of the respective settings of the key parameters and result in smaller losses.
[ Peter B. Webb , Ph.D. ]
FURTHER READING:
American Society for Quality Control. Statistics Division. Glossary and Tables. for Statistical Quality Control. Milwaukee, WI: American Society for Quality Control, 1983.
Anand, K. N. "Development of Process Specification for Radiographic Quality Welding." Quality Engineering, June 1997, 597-601.
Barker, T. B. "Quality Engineering by Design: Taguchi's Philosophy." Quality Progress 19, no. 12 (1986), 32-42.
Box, G. E P., and others. "Quality Practices in Japan." Quality Progress, March 1988, 37-41.
Byrne, Diane M., and Shin Taguchi. "The Taguchi Approach to Parameter Design." ASQC Quality Congress Transaction, 1986, 168-77.
Daniel, Cuthburt. Applications of Statistics to Industrial Experimentation. New York: Wiley, 1976.
Farnum, Nicholas R. Modern Statistical Quality Control and Improvement. New York: Duxbury Press, 1994.
Kackar, R. N. "Off-Line Quality Control, Parameter Design, and the Taguchi Method." Journal of Quality Technology 17, no. 4 (1985): 176-88.
Kros, John F., and Christina M. Mastrangelo. "Impact of Nonquadratic Loss in the Taguchi Design Methodology." Quality Engineering 10, no. 3 (1998): 509-19.
Lochner, Robert H., and Joseph E. Matar. Designing for Quality: An Introduction to the Best of Taguchi and Western Methods of Statistical Experimental Design. Milwaukee, WI: ASQC Quality Press, 1990.
Phadke, M. S. Quality Engineering Using Robust Design. New York: Prentice Hall, 1989.
Quinlan, J. "Product Improvement by Application of Taguchi Method." In Third Supplier Symposium on Taguchi Methods. Dearborn, Ml: American Supplier Institute, 1985.
Ross, P. J. Taguchi Techniques for Quality Engineering. New York: McGraw-Hill, 1988.
Ryan, T. P. "Taguchi's Approach to Experimental Design: Some Concerns." Quality Progress, May 1988, 34-36.
Sonius, M. W., and B. W. Tew. "Design Optimization of Metal to Composite Connections Using Orthogonal Arrays." Quality Engineering 9, no. 3 (1997): 479-87.
Taguchi, Genichi. Introduction to Quality Engineering. White Plains, NY: Asian Productivity Organization, UNIPUB, 1986.
——. "The Development of Quality Engineering." ASI Journal 1, no. 1 (1988): 1-4.
Comment about this article, ask questions, or add new information about this topic: