INPUT-OUTPUT ANALYSIS

Input-output analysis is a basic method of quantitative economics that portrays macroeconomic activity as a system of interrelated goods and services. In particular, the technique observes various economic sectors as a series of inputs of source materials (or services) and outputs of finished or semi-finished goods (or services). The field is most identified with the work of Wassily Leontief (1906-1999), who was awarded the 1973 Nobel Prize in Economics for his pioneering work in the area. Leontief once explained input-output analysis as follows: "When you make bread, you need eggs, flour, and milk. And if you want more bread, you must use more eggs. There are cooking recipes for all the industries in the economy." And hence, one industry's output is another's input, and the chain continues.
INFLUENCE OF CLASSICAL ECONOMICS
Leontief s approach was based in large part on classical theory economics. During the 18th and first half of the 19th centuries the theoretical perspectives of classical school economists held sway in the field. Many of its principal contributors resided or gained notoriety in England. In general, classical theory economists approached the study of economics from the vantage point of its systematic operation, attempting to understand the mutual interaction between parts and whole. This major distinction set them apart from the core theoretical approach taken by present day neoclassical economics which has dominated formal economic analysis since the 1870s. In direct contrast to classical theory, neoclassical theory builds from the level of individual economic agents and conducts its analysis in terms of the operation of individual markets.
The theoretical works of Adam Smith (1723-1790) and David Ricardo (1772-1823) figure most prominently within the school of classical theory. And, while he was critical of and rejected some of their major theoretical propositions, Karl Marx (1818-1883) duly acknowledged the contributions of Smith and Ricardo as instrumental to his own investigation into the systematic operation, as opposed to individual market analysis, of a capitalist economy.
While reviving the methodological approach analogous to classical theorists, Leontief s overriding concern focused on how economic systems were structured, the way an economy's component parts interrelate and mutually influence one another. To a limited extent, because input output analysis deals with aggregate categories, it falls within the purview of macroeconomics. Yet because it is applied within the realm of observable and measured phenomena, input-output analysis is considered a branch of econometrics. As such, much of the existing literature on the subject is highly technical in nature. Practitioners of input-output analysis converse in a seemingly arcane language that few outside its profession know how to interpret. It draws heavily upon mathematics, especially matrix algebra, and, in the construction of input-output tables (see Table 1), strives to be in strict conformity with a bevy of statistical properties. For these reasons alone many students, academics, professionals, and other interested parties find input-output analysis intimidating. Yet the basic approach to the construction of input-output tables and their analysis is highly accessible.
A salient feature of Leontief s early input-output work resided in its highly disaggregated nature. This allowed for a comprehensively detailed, quantitative grasp of the structured linkages between an economic system's component parts. Parallel to his efforts of compiling a highly disaggregated database, Leontief formulated an equally disaggregated theoretical
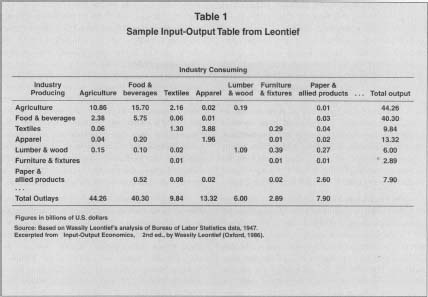
Sample Input-Output Table from Leontief
| Industry Consuming | ||||||||
| Industry Producing | Agriculture | food & beverages | Textiles | Apparel | Lumber & wood | Furniture & fixtures | Paper & allied products … | Total output |
| Agriculture | 10.86 | 15.70 | 2.16 | 0.02 | 0.19 | 0.01 | 44.26 | |
| Food & beverages | 2.38 | 5.75 | 0.06 | 0.01 | 0.03 | 40.30 | ||
| Textiles | 0.06 | 1.30 | 3.88 | 0.29 | 0.04 | 9.84 | ||
| Apparel | 0.04 | 0.20 | 1.96 | 0.01 | 0.02 | 13.32 | ||
| Lumber & wood | 0.15 | 0.10 | 0.02 | 1.09 | 0.39 | 0.27 | 6.00 | |
| Furniture & fixtures | 0.01 | 0.01 | 0.01 | 2.89 | ||||
| Paper & allied products | 0.52 | 0.08 | 0.02 | 0.02 | 2.60 | 7.90 | ||
| Total Outlays | 44.26 | 40.30 | 9.84 | 13.32 | 6.00 | 2.89 | 7.90 | |
| Figures in billions of U.S. dollars | ||||||||
model. For its time, the empirical implementation of his model presented an unsurpassed challenge. Its numerical computations, both in terms of their complexity and scale, were virtually unknown within the field of economics or, for that matter, within any other empirically grounded social science discipline.
Ironically, around the same time Leontief was busy developing input output tables, complete with their aggregative and disaggregative capabilities, the general direction of economic research, under the influence of John Maynard Keynes (1883-1946), became increasingly dominated by a highly aggregative approach. The foremost concern of Keynesian economics was countering the effects of chronic unemployment. This cast a decade's long shadow over Leontief s pathbreaking efforts. Nevertheless, during a time when all the world's advanced capitalist economies were mired in the Great Depression, the emphasis on aggregates, at least from a public policy standpoint, made practical sense.
During the mid-1940s, Leontief acted as a consultant for the U.S. Bureau of Labor Statistics (BLS) when it undertook the first construction of a national input-output table. The effort culminated in the 1947 publication of a 50-sector table of interindustry relations followed shortly thereafter by a 200-sector table with more highly detailed industrial and sectoral classifications. One important practical result of the table was its projections for postwar employment growth until the year 1950 along with policy recommendations should the economy fall short of full employment.
By the early 1950s, though, government appropriations for the BLS's continued development of input-output analysis ceased. A short time later, in 1953, the U.S. Department of Defense abandoned plans to conduct a departmental study using input-output analysis. These decisions were influenced by some businessmen who cast the BLS's program as a step toward socialist "push-button planning." No further work on government sponsored input-output projects transpired until after the Census of Manufactures of 1958. The interindustry results of the input-output study were eventually published in 1964.
Despite its languish in the United States, not long after World War II the use of input-output analysis began to gain an institutional presence throughout the world. Its application soon incorporated major traditional areas of economic analysis such as short-term forecasting, dynamic input-output modeling, income and employment multipliers, regional and interregional analysis, environmental impacts, international trade, underdeveloped economics, and social demography. By 1986, about 90 countries had constructed input-output tables.
HISTORICAL FORERUNNERS
The historical precursors to input-output analysis were in evidence as far back as the first half of the 17th-century. Most economic historians cite Francois Quesnay's (1694-1774) Tableau Economique as the earliest recorded examples to depict the importance of mutual interindustry flows or, in more modem parlance, systematic economic interdependence. Quesnay was one of the leading theoreticians whose work inspired the formation of a group of French agrarian social reformers called the Physiocrats. Though its central focus was on agriculture, the Tableau represents a basic working model of an economy and its extended reproduction. It highlighted the processes of production, circulation of money and commodities, and the distribution of income. And, despite having originally appeared in a cumbersome zigzag form, the Tableau's easy adaptability to Leontief s input-output or double-entry table format has been demonstrated.
The Physiocrats divided society into three classes or sectors. First, a productive class of cultivators engaged in agricultural production were solely responsible for the generation of society's surplus product, a part of which formed net investment. Second, the sterile class referred to producers of manufactured commodities. The term sterile was applied not because manufacturers did not produce anything of value, but because the value of their output (e.g., clothes, shoes, cooking utensils) was presumed to be equal to the necessary costs of raw materials received from the cultivators plus the subsistence level of the producer wages. According to the Physiocrats no surplus product or profits were thought to originate in manufacturing. Lastly came landlords or the idle class who through the money they received as rent consumed the surplus product created by the productive cultivators.
Of particular relevance to the contemporary method of input-output analysis is the Tableau's lengthy depiction of the three classes' transactions. Once the landlord class received their money rents, account was made of the transactions that lead to distribution of products between the agricultural and manufacturing sectors. In short, the Tableau illustrated the two sectors' interdependence as the output from each sector served as a necessary input for the other. These are exactly the type of interindustry relationships that form the core theoretical foundation upon which modem day input-output analysis rests. Here, money's role as a medium of circulation was also critical since it functioned to maintain a fluid means of product allocation. Finally, with the passage of one year, the Ta bleau's entire socioeconomic process came to an end and the transactions were aggregated. Given the Tableau's postulated assumptions, it could then be shown that the economy arrived back at its initial static state.
Some of the outstanding ideas expressed in Quesnay's Tableau were to exercise an enduring impact, even up to the present day, on the study of economics. Among these were: (1) the notion of productive and unproductive labor and their relationship to an economic surplus, (2) the mutual interdependence of production processes, and (3) the circular flows of money and commodities and the potential for economic crises that arise from the hoarding of money. Of these, the second point clearly resonates closest to the object of input-output analysis, while the concern raised by the third point has been addressed by the creation of central banking institutions. However, with the notable exception of two economists, Anwar Shaik and Ertugrul Amhet Tonak, little in the way of integrating the first and second point has been attempted. This is somewhat unsettling as once this distinction has been drawn, comparisons in the measurement of commonly used aggregate macroeconomic input and output variables estimated across the postwar period diverge both in terms of the direction and magnitude of their trends.
Though they were active in England instead of France, the economists who figured most prominently in the development of classical theory themselves drew heavily from theoretical insights of the Physiocratic school. Adam Smith's seminal work, An Inquiry into the Nature and Causes of the Wealth of Nations, borrows wholesale, and proceeds to extend upon, the Physiocrats' major theoretical propositions. And, as Luigi Pasinetti indicated, the analytical roots of Ricardo's now widely used one sector corn model or two sector gold and corn model, depicting economic growth or capital accumulation, takes its notion of economic surplus from the Physiocrats. Both of Ricardo's models also emphasize the Physiocratic notion of production as a circular process, or, in accord with Leontief s definition, of an economy's "general interdependence."
Most of the economic history literature covering the early forerunners of input-output analysis contain a curious omission—hardly any mention of Marx's work. Indeed, of all the economists typically associated with developing the early groundwork out of which input-output analysis was to emerge, probably none spent more time in exploring the interdependence of economic life, along with a host of other related matters, than Marx.
For instance, all the material covered in Volume II of Capital (some 550 pages), analyzes the complete process by which one industry's output serves as another's input. Marx readily acknowledged the debt he owed to Quesnay's Tableau. Called the "reproduction schema," Marx divided total social reproduction into two basic departments: production of the means of production and production of the means of consumption. He then proceeded to elaborate a simple mathematical model to explore what happens when the entire surplus product is totally consumed or used for further accumulation, while in either case balance (equilibrium) between each department is maintained. Simple reproduction referred to the above case where the entire surplus product was consumed while extended reproduction designated the instance where a fraction or all of the surplus product was employed for accumulation purposes.
In his Theories of Surplus-Value, Parts I and III, Marx also devotes over 100 pages to a critique of Quesnay's Tableau and other issues related to Physiocratic theory. Both the Theories of Surplus-Value, and the three volumes of Capital contain much qualified praise for Quesnay's Tableau and other Physiocratic writings which, as Marx pointed out, were to form the theoretical foundation upon which Smith and Ricardo drew.
Leon Walras represents the last link in the chain leading up to Leontief s formulation of input-output analysis. Despite having worked within a neoclassical framework, Walras is credited with introducing the use of production coefficients, a concept that closely resembles one of the core ideas contained in Leontief s work. Yet unlike Leontief s approach, Walras's model of a pure exchange market economy' s ability to arrive at an equilibrium state analytically trivialized the production sector. It treated production as nothing more than an intermediate phase sandwiched between simultaneous acts of utility maximization and the optimal allocation of exogenously given stock of scarce resources. Though it makes little sense to the uninitiated, Walras's use of production coefficients grafted onto this theory of a pure exchange equilibrium suffered from a major limitation. He erroneously treated the stock of resources as a flow variable that occurred within a current period and failed to take account of its existence from previous periods. As a result, Walras was never able to develop a coherent theory of capital accumulation.
LEONTIEF'S DEVELOPMENT OF INPUT-
OUTPUT ANALYSIS
Born 5 August 1906 in St. Petersburg (known as Leningrad during the Communist era), Russia, Leontief received a degree of "Learned Economist" from the University of Leningrad. He received his Ph.D. in 1928 while attending the University of Berlin. Taking up an offer to join the staff of the prestigious National Bureau of Economic Research, Leontief arrived in the United States in 1931. Within a few months he had accepted an appointment at Harvard University where he was to remain and attain worldwide recognition for his invention and application of input-output analysis.
Growing impatient with the penchant of his economist peers for "implicit theorizing," Leontief set out to pursue a dictum that has served as a guiding thread throughout his career: that economic concepts were of little validity unless they could be observed and measured. He was convinced that not only was a well-formulated theory of utmost importance but so too was its application to real economics. To be of use, an With this in mind, Leontief s early extensions of input-output analysis were intended to demonstrate that: (1) production coefficients, expressing relationships among the industrial sectors of an economy, lent themselves to statistical estimation; (2) that the estimated coefficients were sufficiently stable so as to be used in comparative static analyses, i.e., different equilibrium states; and, given the above two points, (3) that on a quantitative level, the merits of different economic policies could be evaluated by taking into consideration both their direct and indirect feedback effects (or multiplier impact) on interindustry flows.
At the time, Leontief s grandiose input-output efforts encountered two major stumbling blocks. First, only part of the information needed for his production coefficients was available (through the U.S. Census of Manufactures) while the remainder had to be arduously gleaned from trade journals and other dispersed sources. Second, underlying Leontief s input-output method was the assumption that production coefficients remained largely constant for extended periods. This proposition was hard to reconcile with the dominant neoclassical theory of production that held that factors of production, (i.e., different quantities of labor and machines expressed in isoquants), were readily substituted for one another as their relative prices changed (i.e., the changing slopes of isocost curves).
Undaunted, around 1934 Leontief began to surmount these self-admitted difficulties. He compiled a 44-sector industrial table containing about 2,000 coefficients in addition to mapping out a plan for their analysis and tests for their validity. To ascertain the coefficients' stability, tables were constructed for the years of 1919 and 1929. The first test results on the coefficients' stability proved inconclusive. This lack of decisiveness was rectified in 1944, however, when Leontief calculated a table of coefficients for 1939, comparable in scope to his 1919 and 1929 tables. He arrived at a satisfactory degree of stability for most coefficients across the two decades.
In 1948, Leontief founded and became the director of the Harvard Economic Research Project established for the purposes of applying and extending the field of input-output analysis. During his 25-year tenure as its director, Leontief remained a driving force in developing interregional input-output analysis and in introducing capital-coefficient matrices meant to depict the investment response to changes in final demand. Given these developments, input-output analysis proved adept at generating an economic system's forecasted growth path as well as its various static equilibrium positions. Leontief s work at the project led to the publication of two books, The Structure of American Economy 1919-1939, in 1951, and Studies in the Structure of the American Economy, in 1953.
Other significant extensions of input-output analysis included estimates of the inflationary consequences of wage settlements, the direct and indirect impact of armament expenditures, estimates of capital requirements for economic development, and methods intended to forecast the individual growth-paths of industrial sectors in a developing economy. In more recent years input-output analysis has been applied to the issue of worldwide economic growth, its environmental consequences, its impact on the world's reserve of natural resources, and the political-economic ramifications for relations between the economies of developed and less-developed countries. Under a project funded by the United Nations, Leontief managed a study on the growth of the world economy until the year 2000. The multiregional input-output model extended across 15 regions consisting of 45 sectors each with balanced trading accounts.
The results were published in 1977 as The Future of the World Economy. Based on a broad set of reasonable assumptions, it provisionally concluded that only small progress would be made in closing the gap between rich and poor regions unless current policies dealing with international trade and finance were abandoned. As policy alternatives the study recommended a marked increase in multinational aid and a significant increase in the flow of imports from the developing economies to industrial economies.
DEVELOPMENTS AND EXTENSIONS
A standard input-output table contains an equal number of rows and
columns, as depicted in Table 1, which is based on an early input-output
table produced by Leontief in 1951. Tables can measure dollars or physical
units of produced goods and services, such as tons of steel, bushels of
wheat, or gallons of fuel. Following the construction of an annual
input-output table, it is possible to derive a second table of input or
technical coefficients. The term "technical coefficients"
refers to the quantity of inputs required from each industry to produce
one dollar's worth of a given industry's output. Because it
represents the entire domain of wealth-producing activities, computation
of the technical coefficients are restricted to the processing sector
industries only. The coefficients can be denominated in either monetary or
physical units. The basic formula for determining coefficients is
where
a
ij
= the input coefficient of industry
i
into industry
j,
X
ij
= the amount of industry
i
's output used by industry
j,
and
x
j
= the total output from industry
j
Using this formula, the coefficient a ij can be obtained for all the industries in an input-output table. Once a transaction table of direct and indirect coefficients (or a coefficient matrix) has been obtained, several common economic analyses can be performed.
FORECASTS BASED ON COEFFICIENTS.
The first concerns the use of static input-output tables to consistently forecast projections of both industry and final sector demands. Typically, for periods of up to two or three years, these are reliable short-term forecasts over which it makes sense to assume that the production coefficients change very little. But the existence of stable technical coefficients within a longer term forecast is tenuous. Integration of disturbances related to relative input price changes, the appearance of new industries during the projection period, and the effects of technological change on technical coefficients, require more complex, dynamic models of input output analysis. Around 1953 Leontief initially formulated a dynamic input-output model. Later, Copper Almon also achieved significant results working with dynamic input-output models.
INCOME MULTIPLIERS.
A second area extending the use of input-output analysis concerns the use of income multipliers. Their construction requires appending the households row and column to a coefficient table followed by the calculation of their direct and indirect effects. While Keynes first introduced and applied multipliers as a concept central to the study of macroeconomics, it was R.S. Kahn who originated their theoretical development. Nevertheless, credit goes to input-output analysis for making it possible to disaggregate the highly aggregated multipliers in order to detail how multiplier effects ramify throughout an economic structure. If, for instance, it becomes a question as to whether a given level of public investment should be directed toward the construction or military industries, then, based on their different multiplier impacts, input output analysis provides policy makers with a tool to evaluate the merits of either project. Or, in international trade, should the problem concern easing import restrictions, input-output analysis can indicate how imports might affect industries supplying domestic inputs and outputs.
In short, when based on the assumption that each industry's output expands by the same amount, then input-output augmented multipliers reveal that varying amounts of income are generated by different industries. In general, for the case of international trade, the greater the degree of the domestic economy's interdependence, the greater will be the direct effects of income change. But in terms of both the direct and indirect effects the results could be reversed, neutralized, or strengthened.
EMPLOYMENT MULTIPLIERS.
Third, the existence of an input-output table combined with a projected change in aggregate final demand also allows for the calculation of employment multipliers. Computation of employment multipliers differ from the method used for income multipliers. Two methods, the Isard-Kuene and Moore-Peterson approach, were the first to tackle the subject. The Isard-Kuene method sought to measure the total employment impact within a region based on the establishment of a new basic industry within it borders. It drew from national coefficients to estimate the inputs of both the basic industry and the accompanying industries expected to locate around the new industry. The Moore-Peterson method, by contrast, uses regional—instead of national—coefficients to estimate both the direct, indirect, and induced employment effects. Assuming a change in the final demand for the output of one or more industries within the region, calculation of total employment changes was performed across all industries.
REGIONAL INPUT-OUTPUT ANALYSIS.
Developments in both regional and interregional models of input-output studies have loomed large in the post-World War II era. During this time the trend in economics has moved to quantitative research, a task for which input-output analysis is well suited. The distinction between the two models is straightforward, a region comprises one geographical area while an interregional model spans several regions. From here two further complementary distinctions apply—that between a balanced regional and pure interregional model. A balanced regional model is constructed through disaggregation of a national input-output model into component regions. Conversely, a pure interregional model is designed by aggregating a number of regional tables, which may or may not include all the regions in a national economy.
Interregional models have been used to analyze regional balance of trade payments and interregional trade flows. Interregional models are more complex than either national or regional models. This stems from having to sort out interindustry and interregional economic flows. As a result many have tended to be highly aggregated since reliable data on industry sales and purchases by region are hard to come by.
Regional models cover geographic areas of varying size. Some have encompassed Federal Reserve districts, others, metropolitan areas, states, counties, or an area specified across two or more states. For the most part, regional input-output models are considered more "open" than a national economy model. The quality of openness derives from the tendency of regions to be more highly specialized in terms of their processing sectors, thus more inclined to transact ex-changes from without.
CURRENT STATUS AND TRENDS
Input-output analysis remains an active branch of economics, and one with numerous offshoots. Some of its most popular applications are those that Leontief helped pioneer, including national accounts and trade, environmental studies, and technological change forecasts. In addition to the many input-output studies published from time to time in general economics journals, there are a number of academic journals devoted specifically to input-output analysis. For economists who specialize in input-output work, there are also several professional associations worldwide, the most prominent being the International Input-Output Association (IIOA), based in Vienna, Austria. As of the late 1990s, the IIOA had some 300 individual members and 20 institutional members representing 49 nations.
Input-output analysis has sustained such interest in the professional community because of its versatility and its strong grounding in empirical evidence. While it is most associated with grand macroeconomic studies like those of Leontief, input-output analysis can be equally valuable to research on a single firm. And unlike some areas of economics, input-output analysis does not come with a great deal of theoretical baggage that is hard to prove in real life. Of course, it is susceptible to distortions from measurement error or inaccurate modeling, but its underlying strength lies in being driven by real data.
[ Daniel E King ]
FURTHER READING:
Correa, Hector, and James Craft. "Input-Output Analysis for Organizational Human Resources Management." Omega, February 1999.
Galbraith, James. "Wassily Leontief: An Appreciation." Challenge, May-June 1999.
Kurz, Heinz D., Erik Dietzenbacher, and Christian Lager, eds. Input-Output Analysis. Cheltenham, UK: Edward Elgar Publishing, 1998.
Leontief, Wassily. Input-Output Economics. 2nd ed. New York: Oxford University Press, 1986.
Shaik, Anwar, and Ertugrul A. Tonak. Measuring the Wealth of Nations: The Political Economy of National Accounts. New York: Columbia University Press, 1994.
Sohn, Ira, ed. Readings in Input-Output Analysis: Theory and Applications. New York: Oxford University Press, 1986.
I hereby wish to ask for further computational formulas for the subject INPUT-OUTPUT Analysis