INVENTORY MANAGEMENT

Inventory management, or inventory control, is an attempt to balance inventory needs and requirements with the need to minimize costs resulting from obtaining and holding inventory. There are several schools of thought that view inventory and its function differently. These will be addressed later, but first we present a foundation to facilitate the reader's understanding of inventory and its function.
WHAT IS INVENTORY?
Inventory is a quantity or store of goods that is held for some purpose or use (the term may also be used as a verb, meaning to take inventory or to count all goods held in inventory). Inventory may be kept "in-house," meaning on the premises or nearby for immediate use; or it may be held in a distant warehouse or distribution center for future use. With the exception of firms utilizing just-in-time methods, more often than not, the term "inventory" implies a stored quantity of goods that exceeds what is needed for the firm to function at the current time (e.g., within the next few hours).
WHY KEEP INVENTORY?
Why would a firm hold more inventory than is currently necessary to ensure the firm's operation? The following is a list of reasons for maintaining what would appear to be "excess" inventory.
| January | February | March | April | May | June | |
| Demand | 50 | 50 | 0 | 100 | 200 | 200 |
| Produce | 100 | 100 | 100 | 100 | 100 | 100 |
| Month-end inventory | 50 | 100 | 200 | 200 | 100 | 0 |
MEET DEMAND.
In order for a retailer to stay in business, it must have the products that the customer wants on hand when the customer wants them. If not, the retailer will have to back-order the product. If the customer can get the good from some other source, he or she may choose to do so rather than electing to allow the original retailer to meet demand later (through back-order). Hence, in many instances, if a good is not in inventory, a sale is lost forever.
KEEP OPERATIONS RUNNING.
A manufacturer must have certain purchased items (raw materials, components, or subassemblies) in order to manufacture its product. Running out of only one item can prevent a manufacturer from completing the production of its finished goods.
Inventory between successive dependent operations also serves to decouple the dependency of the operations. A machine or workcenter is often dependent upon the previous operation to provide it with parts to work on. If work ceases at a workcenter, then all subsequent centers will shut down for lack of work. If a supply of work-in-process inventory is kept between each workcenter, then each machine can maintain its operations for a limited time, hopefully until operations resume the original center.
LEAD TIME.
Lead time is the time that elapses between the placing of an order (either a purchase order or a production order issued to the shop or the factory floor) and actually receiving the goods ordered.
If a supplier (an external firm or an internal department or plant) cannot supply the required goods on demand, then the client firm must keep an inventory of the needed goods. The longer the lead time, the larger the quantity of goods the firm must carry in inventory.
A just-in-time (JIT) manufacturing firm, such as Nissan in Smyrna, Tennessee, can maintain extremely low levels of inventory. Nissan takes delivery on truck seats as many as 18 times per day. However, steel mills may have a lead time of up to three months. That means that a firm that uses steel produced at the mill must place orders at least three months in advance of their need. In order to keep their operations running in the meantime, an on-hand inventory of three months' steel requirements would be necessary.
HEDGE.
Inventory can also be used as a hedge against price increases and inflation. Salesmen routinely call purchasing agents shortly before a price increase goes into effect. This gives the buyer a chance to purchase material, in excess of current need, at a price that is lower than it would be if the buyer waited until after the price increase occurs.
QUANTITY DISCOUNT.
Often firms are given a price discount when purchasing large quantities of a good. This also frequently results in inventory in excess of what is currently needed to meet demand. However, if the discount is sufficient to offset the extra holding cost incurred as a result of the excess inventory, the decision to buy the large quantity is justified.
SMOOTHING REQUIREMENTS.
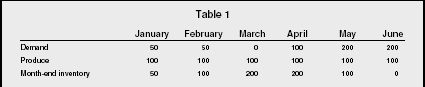
Sometimes inventory is used to smooth demand requirements in a market where demand is somewhat erratic. Consider the demand forecast and production schedule outlined in Table 1.
Notice how the use of inventory has allowed the firm to maintain a steady rate of output (thus avoiding the cost of hiring and training new personnel), while building up inventory in anticipation of an increase in demand. In fact, this is often called anticipation inventory. In essence, the use of inventory has allowed the firm to move demand requirements to earlier periods, thus smoothing the demand.
CONTROLLING INVENTORY
Firms that carry hundreds or even thousands of different part numbers can be faced with the impossible task of monitoring the inventory levels of each part number. In order to facilitate this, many firm's use an ABC approach. ABC analysis is based on Pareto Analysis, also known as the "80/20" rule. The 80/20 comes from Pareto's finding that 20 percent of the populace possessed 80 percent of the wealth. From an inventory perspective it can restated thusly: approximately 20 percent of all inventory items represent 80 percent of inventory costs. Therefore, a firm can control 80 percent of its inventory costs by monitoring and controlling 20 percent of its inventory. But, it has to be the correct 20 percent.
The top 20 percent of the firm's most costly items are termed "A" items (this should approximately represent 80 percent of total inventory costs). Items that are extremely inexpensive or have low demand are termed "C" items, with "B" items falling in between A and C items. The percentages may vary with each firm, but B items usually represent about 30 percent of the total inventory items and 15 percent of the costs. C items generally constitute 50 percent of all inventory items but only around 5 percent of the costs.
By classifying each inventory item as an A, B or C the firm can determine the resources (time, effort and money) to dedicate to each item. Usually this means that the firm monitors A items very closely but can check on B and C items on a periodic basis (for example, monthly for B items and quarterly for C items).
Another control method related to the ABC concept is cycle counting. Cycle counting is used instead of the traditional "once-a-year" inventory count where firms shut down for a short period of time and physically count all inventory assets in an attempt to reconcile any possible discrepancies in their inventory records. When cycle counting is used the firm is continually taking a physical count but not of total inventory.
A firm may physically count a certain section of the plant or warehouse, moving on to other sections upon completion, until the entire facility is counted. Then the process starts all over again.
The firm may also choose to count all the A items, then the B items, and finally the C items. Certainly, the counting frequency will vary with the classification of each item. In other words, A item may be counted monthly, B items quarterly, and C items yearly. In addition the required accuracy of inventory records may vary according to classification, with A items requiring the most accurate record keeping.
BALANCING INVENTORY AND COSTS
As stated earlier, inventory management is an attempt to maintain an adequate supply of goods while minimizing inventory costs. We saw a variety of reasons companies hold inventory and these reasons dictate what is deemed to be an adequate supply of inventory. Now, how do we balance this supply with its costs? First let's look at what kind of costs we are talking about.
There are three types of costs that together constitute total inventory costs: holding costs, set-up costs, and purchasing costs.
HOLDING COSTS.
Holding costs, also called carrying costs, are the costs that result from maintaining the inventory. Inventory in excess of current demand frequently means that its holder must provide a place for its storage when not in use. This could range from a small storage area near the production line to a huge warehouse or distribution center. A storage facility requires personnel to move the inventory when needed and to keep track of what is stored and where it is stored. If the inventory is heavy or bulky, forklifts may be necessary to move it around.
Storage facilities also require heating, cooling, lighting, and water. The firm must pay taxes on the inventory, and opportunity costs occur from the lost use of the funds that were spent on the inventory. Also, obsolescence, pilferage (theft), and shrinkage are problems. All of these things add cost to holding or carrying inventory.
If the firm can determine the cost of holding one unit of inventory for one year ( H ) it can determine its annual holding cost by multiplying the cost of holding one unit by the average inventory held for a one-year period. Average inventory can be computed by dividing the amount of goods that are ordered every time an order is placed ( Q ) by two. Thus, average inventory is expressed as Q /2. Annual holding cost, then, can be expressed as H ( Q /2).
SET-UP COSTS.
Set-up costs are the costs incurred from getting a machine ready to produce the desired good. In a manufacturing setting this would require the use of a skilled technician (a cost) who disassembles the tooling that is currently in use on the machine. The disassembled tooling is then taken to a tool room or tool shop for maintenance or possible repair (another cost). The technician then takes the currently needed tooling from the tool room (where it has been maintained; another cost) and brings it to the machine in question.
There the technician has to assemble the tooling on the machine in the manner required for the good to be produced (this is known as a "set-up"). Then the technician has to calibrate the machine and probably will run a number of parts, that will have to be scrapped (a cost), in order to get the machine correctly calibrated and running. All the while the machine has been idle and not producing any parts (opportunity cost). As one can see, there is considerable cost involved in set-up.
If the firm purchases the part or raw material, then an order cost, rather than a set-up cost, is incurred. Ordering costs include the purchasing agent's salary and travel/entertainment budget, administrative and secretarial support, office space, copiers and office supplies, forms and documents, long-distance telephone bills, and computer systems and support. Also, some firms include the cost of shipping the purchased goods in the order cost.
If the firm can determine the cost of one set-up ( S ) or one order, it can determine its annual setup/order cost by multiplying the cost of one set-up by the number of set-ups made or orders placed annually. Suppose a firm has an annual demand ( D ) of 1,000 units. If the firm orders 100 units ( Q ) every time it places and order, the firm will obviously place 10 orders per year ( D / Q ). Hence, annual set-up/order cost can be expressed as S ( D / Q ).
PURCHASING COST.
Purchasing cost is simply the cost of the purchased item itself. If the firm purchases a part that goes into its finished product, the firm can determine its annual purchasing cost by multiplying the cost of one purchased unit ( P ) by the number of finished products demanded in a year ( D ). Hence, purchasing cost is expressed as PD.
Now total inventory cost can be expressed as:
Total = Holding cost + Set-up/Order cost + Purchasing cost
or
Total =
H
(
Q
/2) +
S
(
D
/
Q
) +
PD
If holding costs and set-up costs were plotted as lines on a graph, the
point at which they intersect (that is, the point at which they are equal)
would indicate the lowest total inventory cost. Therefore, if we want to
minimize total inventory cost, every time we place an order, we should
order the quantity (
Q
) that corresponds to the point where the two values are equal. If we set
the two costs equal and solve for
Q
we get:
H
(
Q
/2) =
S
(
D
/
Q
)
Q
= 2
DS
/
H
The quantity
Q
is known as the economic order quantity (EOQ). In order to minimize total
inventory cost, the firm will order
Q
every time it places an order. For example, a firm with an annual demand
of 12,000 units (at a purchase price of $25 each), annual holding cost of
$10 per unit and an order cost of $150 per order (with orders placed once
a month) could save $800 annually by utilizing the EOQ. First, we
determine the total costs without using the EOQ method:
Q
= $10(1000/2) + $150(12,000/1000) + $25(12,000) = $306,800
Then we calculate EOQ:
EOQ = 2(12,000)($150)/$10= 600
And we calculate total costs at the EOQ of 600:
Q
= $10(600/2) + $150(12,000/600) + $25(12,000) = $306,000
Finally, we subtract the total cost of
Q
from
Q
to determine the savings:
$306,800 − 306,000 = $800
Notice that if you remove purchasing cost from the equation, the savings is still $800. We might assume this means that purchasing cost is not relevant to our order decision and can be eliminated from the equation. It must be noted that this is true only as long as no quantity discount exists. If a quantity discount is available, the firm must determine whether the savings of the quantity discount are sufficient to offset the loss of the savings resulting from the use of the EOQ.
There are a number of assumptions that must be made with the use of the EOQ. These include:
- Only one product is involved.
- Deterministic demand (demand is known with certainty).
- Constant demand (demand is stable through-out the year).
- No quantity discounts.
- Constant costs (no price increases or inflation).
While these assumptions would seem to make EOQ irrelevant for use in a realistic situation, it is relevant for items that have independent demand. This means that the demand for the item is not derived from the demand for something else (usually a parent item for which the unit in question is a component). For example, the demand for steering wheels would be derived from the demand for automobiles (dependent demand) but the demand for purses is not derived from anything else; purses have independent demand.
OTHER LOT-SIZING TECHNIQUES
There are a number of other lot-sizing techniques available in addition to EOQ. These include the fixed-order quantity, fixed-order-interval model, the single-period model, and part-period balancing.
FIXED-ORDER-QUANTITY MODEL.
EOQ is an example of the fixed-order-quantity model since the same quantity is ordered every time an order is placed. A firm might also use a fixed-order quantity when it is captive to packaging situations. If you were to walk into an office supply store and ask to buy 22 paper clips, chances are you would walk out with 100 paper clips. You were captive to the packaging requirements of paper clips, i.e., they come 100 to a box and you cannot purchase a partial box. It works the same way for other purchasing situations. A supplier may package their goods in certain quantities so that their customers must buy that quantity or a multiple of that quantity.
FIXED-ORDER-INTERVAL MODEL.
The fixed-order-interval model is used when orders have to be placed at fixed time intervals such as weekly, biweekly, or monthly. The lot size is dependent upon how much inventory is needed from the time of order until the next order must be placed (order cycle). This system requires periodic checks of inventory levels and is used by many retail firms such as drug stores and small grocery stores.
SINGLE-PERIOD MODEL.
The single-period model is used in ordering perishables, such as food and flowers, and items with a limited life, such as newspapers. Unsold or unused goods are not typically carried over from one period to another and there may even be some disposal costs involved. This model tries to balance the cost of lost customer goodwill and opportunity cost that is incurred from not having enough inventory, with the cost of having excess inventory left at the end of a period.
PART-PERIOD BALANCING.
Part-period balancing attempts to select the number of periods covered by the inventory order that will make total carrying costs as close as possible to the set-up/order cost.
When a proper lot size has been determined, utilizing one of the above
techniques, the reorder point, or point at which an order should be
placed, can be determined by the rate of demand and the lead time. If
safety stock is necessary it would be added to the reorder point quantity.
Reorder point =
Expected demand during lead time + Safety stock
Thus, an inventory item with a demand of 100 per month, a two-month lead
time and a desired safety stock of two weeks would have reorder point of
250. In other words, an order would be placed whenever the inventory level
for that good reached 250 units.
Reorder point =
100/month × 2 months + 2 weeks' safety stock = 250
OTHER SCHOOLS OF THOUGHT
IN INVENTORY MANAGEMENT
There are a number of techniques and philosophies that view inventory management from different perspectives.
MRP AND MRP II.
MRP and MRP II are computer-based resource management systems designed for items that have dependent demand. MRP and MRP II look at order quantities period by period and, as such, allow discrete ordering (ordering only what is currently needed). In this way inventory levels can be kept at a very low level; a necessity for a complex item with dependent demand.
JUST-IN-TIME (JIT).
Just-in-time (JIT) is a philosophy that advocates the lowest possible levels of inventory. JIT espouses that firms need only keep inventory in the right quantity at the right time with the right quality. The ideal lot size for JIT is one, even though one hears the term "zero inventory" used.
THEORY OF CONSTRAINTS (TOC).
Theory of constraints (TOC) is a philosophy which emphasizes that all management actions should center around the firm's constraints. While it agrees with JIT that inventory should be at the lowest level possible in most instances, it advocates that there be some buffer inventory around any capacity constraint (e.g., the slowest machine) and before finished goods.
THE FUTURE OF INVENTORY
MANAGEMENT
The advent, through altruism or legislation, of environmental management has added a new dimension to inventory management-reverse supply chain logistics. Environmental management has expanded the number of inventory types that firms have to coordinate. In addition to raw materials, work-in-process, finished goods, and MRO goods, firms now have to deal with post-consumer items such as scrap, returned goods, reusable or recyclable containers, and any number of items that require repair, reuse, recycling, or secondary use in another product. Retailers have the same type problems dealing with inventory that has been returned due to defective material or manufacture, poor fit, finish, or color, or outright "I changed my mind" responses from customers.
Finally, supply chain management has had a considerable impact on inventory management. Instead of managing one's inventory to maximize profit and minimize cost for the individual firm, today's firm has to make inventory decisions that benefit the entire supply chain.
SEE ALSO: Aggregate Planning ; Inventory Types ; Lean Manufacturing and Just-in-Time Production ; Manufacturing Resources Planning ; Reverse Supply Chain Logistics ; Supply Chain Management
R. Anthony Inman
FURTHER READING:
Biederman, David. "Reversing Inventory Management." Traffic World (12 December 2004): 1.
Stevenson, William J. Production Operations Management. Boston, MA: Irwin/McGraw-Hill, 2005.
Sucky, Eric. "Inventory Management in Supply Chains: A Bargaining Problem." International Journal of Production Economics 93/94: 253.
Thanks