DURATION
Duration is a measure of the price sensitivity of a fixed income security
to changes in the interest rate. It was developed by Frederick R. Macaulay
in 1938 to replace the inferior price sensitivity to interest rate change
methods: term to maturity and weighted average term to maturity. Duration
is a form of the weighted average term to maturity. The mathematical
expression to define duration is:
where C, is the cash flow (interest or principal payment),
t
is the time of the cash flow,
m
is the length of time to the final maturity of the fixed income security,
i
is the interest rate (yield to maturity) of the fixed income security,
expressed in decimal form.
That is, duration is the sum of the present value of each cash flow multiplied by the time period when it occurs divided by the current price of the instrument.
For example, a bond has a 6 percent coupon interest rate (paid annually) with five years left to
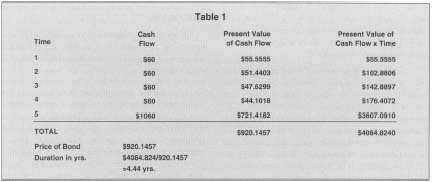
| Time | Cash Flow | Present Value of Cash Flow | Present Value of Cash Flow x Time |
| 1 | $60 | $55.5555 | $55.5555 |
| 2 | $60 | $51.4403 | $102.8806 |
| 3 | $60 | $47.6299 | $142.8897 |
| 4 | $60 | $44.1018 | $176.4072 |
| 5 | $1060 | $721.4182 | $3607.0910 |
| TOTAL | $920.1457 | $4084.8240 | |
| Price of Bond | $920.1457 | ||
| Duration in yrs. | $4084.824/920.1457=4.44 yrs. |
maturity when it repays the face value (principal) of $ 1,000. The current market interest rate (yield to maturity) is 8 percent. What is the duration? Table 1 illustrates this.
The importance of duration is that it tells us how much the price of a fixed income security will change by, given a change in interest rates. To be precise, the modified duration is used. The modified duration is the duration divided by the quantity one plus the interest rate (in decimal form).
Thus, the percentage change in price of a fixed income security equals the modified duration multiplied by the percentage change in interest rates. Of course, the price moves in opposite direction to the interest rate change.
That is, mathematically,
To illustrate, what would happen to the price of the $920.1457 bond if interest rates changed by 1 percent? The modified duration is 4.11 years [4.44/(1 + .08)]. Therefore, the bond price would decrease by 4.11 percent to a price of $882.33.
Other considerations impacting on the degree of duration include call or put clauses and other early retirement features as well as other means of altering the payment pattern.
Besides having a measure that tells us how much the price changes for an interest rate change, the investor can acquire a portfolio to take advantage of an interest rate forecast. For example, if interest rates were predicted to drop, a long-duration bond portfolio would be ideal to maximize return. On the other hand, some investors desire to protect themselves against interest rate fluctuations. In this situation, the portfolio would need to be immunized against interest rate volatility. The use of duration would help to achieve the optimal bond strategy to prevent wealth losses that would occur in the face of increasing interest rates.
More recently, spectacular financial losses and failures have been reported by companies engaging in financial innovations such as derivative securities. Some of the derivatives with extraordinary duration measures are inverse floaters and collateralized mortgage obligations (CMO). These financial instruments can be designed to have a negative duration or extremely large duration values or both. This makes for tremendous price volatility on minute interest rate changes and therefore extremely risky investments.
[ Raymond A. K. Cox ]
FURTHER READING:
Babbell, David F., Craig Merrill, and William Panning. "Default Risk and the Effective Duration of Bonds." Financial Analysts Journal 53, no. I (January/February 1997): 35-44.
Cox, Raymond A. K., and Rose M. Prasad. "Strategies for Banks to Cope with Changing Interest Rates." Review of Business 14, no. I (summer/fall 1992): 14-18.
Macaulay, Frederick R. Some Theoretical Problems Suggested by the Movement of Interest Rates, Bond Yields, and Stock Prices in the United States since 1865. New York: National Bureau of Economic Research, 1938.
Comment about this article, ask questions, or add new information about this topic: