DECISION SUPPORT SYSTEMS

Decision support systems (DSS) are computer information systems that perform complex data analysis in order to help users make informed decisions. In general, a DSS retrieves information from a large data warehouse, analyzes it in accordance with user specifications, then publishes the results in a format that users can readily understand and use. DSS find application in a wide range of business settings, including investment portfolio management.
Portfolio management is one of the most essential problems in modern financial theory. It involves the construction of a portfolio of securities (stocks, bonds, treasury bills, etc.) that maximizes the investor's utility. The process leading to the construction of such a portfolio consists of two major steps. In the first step the decision-maker (investor, portfolio manager) has to evaluate the securities that are available as investment instruments. The vast number of available securities, especially in the case of stocks, makes this step necessary, in order to focus the analysis on a limited number of the best investment choices. Thus, on the basis of this evaluation stage the decision-maker selects a small number of securities that constitute the best investment opportunities. In the second step of the process the decision maker must decide on the amount of the available capital that should be invested in each security, thus constructing a portfolio of the selected securities. The portfolio should be constructed in accordance with the decision-maker's investment policy and risk tolerance.
The portfolio theory assumes that the decision-maker's judgment and investment policy can be represented by a utility function that is implicitly used by the decision-maker in making his investment decisions. Thus, the maximization of this utility function will result in the construction of a portfolio that is as consistent as possible with the decision-maker's expectations and investment policy. However, it is quite difficult to determine the specific form of this utility function.
The founder of portfolio theory, Nobelist Harry Markowitz, has developed a framework according to which the decision-maker's utility is a function of two variables, the expected return of the portfolio and its risk. Thus, he formulated the maximization of the decision-maker's utility as a two-objective problem: maximizing the expected return of the portfolio and minimizing the corresponding risk. To consider the return and the risk, Markowitz used two well-known statistical measures, the mean of all possible returns to estimate the return of the portfolio, and the variance to measure its risk. On the basis of this mean-variance framework, Markowitz has developed a mathematical framework to identify the efficient set of portfolios that maximizes returns at any given level of allowable risk. Given the risk aversion policy of the investor, it is possible to select the most appropriate portfolio from the efficient set.
This pioneering work of Markowitz motivated financial researchers to develop new portfolio management techniques, and significant contributions have been made over the last decades. The most significant of the approaches that have been proposed for portfolio management include the capital asset pricing model (CAPM), the arbitrage pricing theory (APT), single and multi index models, as well as several optimization techniques. Elton and Gruber's 1995 book Modern Portfolio Theory and Investment Analysis provides a comprehensive discussion of the various approaches.
DECISION SUPPORT SYSTEMS
IN PORTFOLIO MANAGEMENT
The concept of decision support systems (DSS) was introduced, from a theoretical point of view, in the late 1960s. DSS can be defined as computer information systems that provide information in a specific problem domain using analytical decision models and techniques, as well as access to databases, in order to support a decision maker in making decisions effectively in complex and ill-structured problems. Thus, the basic goal of DSS is to provide the necessary information to the decision-maker in order to help him or her get a better understanding of the decision environment and the alternatives available.
A typical structure of a DSS includes three main parts: the database, the model base, and the user interface. The database includes all the information and data that are necessary to perform the analysis on the decision problem at hand. Data entry, storage, and retrieval are performed through a database management system. The model base is an arsenal of methods, techniques, and models that can be used to perform the analysis and support the decision-maker. These models or techniques are applied to the raw data in order to produce analysis or more meaningful output for the decision-maker. A model base management system is responsible for performing all tasks that are related to model management, such as model development, updates, storage, and retrieval. Finally, the user interface is responsible for the communication between the user and the system, while it further serves as a link between the database and the model base. The appropriate design of the user interface is a key issue towards the successful implementation of the whole system, so as to ensure that the user can take full advantage of the analytical capabilities that the system provides. Advances in computer hardware and software have enabled user-friendly graphical user interfaces (GUIs) to serve this function.
During the last four decades DSS have been developed and implemented to tackle a variety of real world decision-making problems, including financial problems and portfolio management. The portfolio management process involves the analysis of a vast volume of information and data, including financial, stock market, and macroeconomic data. Analyzing a continuous flow of such a vast amount of information for every available security in order to make real time portfolio management decisions is clearly impossible with out the support of a specifically designed computer system that will facilitate not only the data management process, but also the analysis.
Thus, the contribution of DSS to portfolio management becomes apparent. They provide an integrated tool to perform real-time analyses of portfolio management related data, and provide information according to the decision-maker's preferences. Furthermore, they enable the decision-maker to take full advantage of sophisticated analytic methods, including multivariate statistical and econometric techniques, powerful optimization methods, advanced preference modeling, and multiple-criteria decision-making techniques. DSS incorporating multiple-criteria decision-making methods in their structure are known as multicriteria DSS, and they have found several applications in the field of finance. Zopounidis, Godefroid, and Hurson have presented the methodological framework for the design and development of a multicriteria DSS for portfolio management. The use of such innovative tools in portfolio management decision making, together with the tools provided by the modern portfolio theory (CAPM, APT, etc.), provide the basis for improving the portfolio management process. The subsequent section illustrates the capabilities that a multicriteria DSS can provide in portfolio management through the presentation of the Investor system.
PORTFOLIO MANAGEMENT DSS
IN PRACTICE: AN ILLUSTRATION
OF THE INVESTOR SYSTEM
The Investor system is a DSS designed and developed to support the portfolio management process and to help construct portfolios of stocks. The system includes a combination of portfolio theory models, multivariate statistical methods, and multiple criteria decision-making techniques for stock evaluation and portfolio construction. The structure of the system is presented in Figure 1.
FINANCIAL DATA.
The database of the system includes four types of information and data. The first involves the financial statements of the firms whose stocks are considered in the portfolio management problem. The balance sheet and the income statement provide valuable information regarding the financial soundness of the firms (e.g., sales, net profit, net worth, liabilities, assets, etc.). The system contains such financial data spanning a five-year period, so that users can reach informed conclusions about the firms' financial evolution.
QUALITATIVE INFORMATION.
In addition to these financial data, information on some qualitative factors is also inserted in the database. The management of the firms, their organization, their reputation in the market, their technical facilities, and their market position affect directly the operation and the performance of the firms; thus, they constitute fundamental factors in the analysis of the firms whose stocks that are considered in the portfolio management problem.
MARKET DATA.
The third type of information included in the database involves the stocks' market histories. This information involves the stock prices, the marketability of the stocks, their beta coefficient (a measure of risk representing the relationship between the changes in the price of individual stocks with the changes in the market), the dividend yield, the price/earnings ratio, and so forth.
MACROECONOMIC DATA.
Finally, information regarding the macroeconomic environment is also included. Inflation, interest rates, exchange rates, and other macroeconomic variables have a direct impact on the performance of the stock market, thus potentially affecting any individual stock. The combination of this information with the financial and stock histories of individual firms enables portfolio managers to perform a global evaluation of the investment opportunities available, both in terms of their sensitivity and
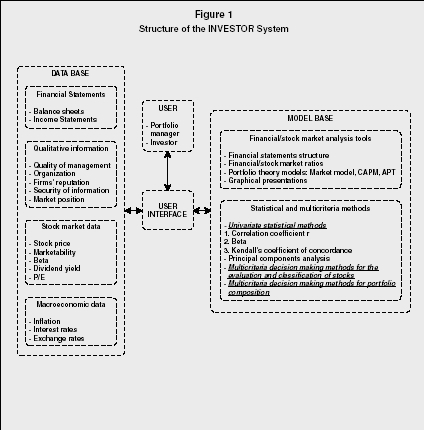
Structure of the INVESTOR System
ANALYSIS TOOLS.
The analysis of all this information is performed through the tools incorporated in the system's model base. Two major components can be distinguished in the model base. The first one consists of financial and stock market analysis tools. These can analyze the structure of the financial statements of the firms, calculate financial and stock market ratios, apply well-known portfolio theory models (e.g., the market model, the CAPM, the APT), and present several graphical summaries of the results obtained through these tools to facilitate drawing some initial conclusions about the stocks' performance.
The second component of the model base involves more sophisticated analysis tools, including statistical and multiple-criteria decision-making techniques. More specifically, univariate statistical techniques are used to measure the stability of the beta coefficient of the stocks, while principal components analysis (a multivariate technique) is used to identify the most significant factors or criteria that describe the performance of the stocks, and to place the stocks into homogeneous groups according to their financial and stock market characteristics. The criteria identified as most crucial can be used to evaluate the stocks and thereby construct a portfolio that meets the investment policy of the investor/portfolio manager. Of course, the portfolio manager interacts with the system, and he or she can also introduce into the analysis the evaluation criteria that he or she considers important, even if these criteria are not found significant by principal components analysis.
The evaluation of the stocks' performance is completed through multiple-criteria decision-making
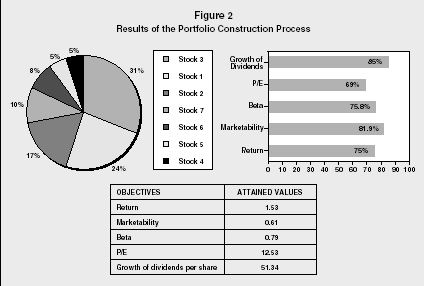
Results of the Portfolio Construction Process
On the basis of this classification, the investor/portfolio manager can select a limited number of stocks to include in the actual portfolio, which represent the best investment opportunities. Constructing the portfolio is accomplished through multiple-criteria decision-making techniques that are appropriate for optimizing a set of objective functions subject to some constraints. The objective functions represent the investor/portfolio manager's objectives on some evaluation criteria (return, beta, marketability, etc.), while constraints can be imposed to ensure that the constructed portfolio meets some basic aspects of the investment policy of the investor/portfolio manager.
For instance, the investor/portfolio manager can introduce constraints on the amount of capital invested in stocks of specific business sectors, the amount of capital invested in high-risk or low-risk stocks (high and low β coefficient, respectively), to determine a minimum level of return or a maximum level of risk, and so on. Once such details are determined, an interactive and iterative optimization procedure is performed that leads to the construction of a portfolio of stocks that meets the investor's investment policy and preferences. The results presented through the screen of Figure 2 show the proportion of each stock in the constructed portfolio, the performance of the portfolio on the specified evaluation criteria (attained values), as well as the rate of closeness (achievement rate) of the performance of the portfolio as opposed to the optimal values on each evaluation criterion (the higher this rate is, the closer the performance of the portfolio to the optimal one for each criterion).
Since the development of the portfolio theory in the 1950s, portfolio management has gained increasing interest within the financial community. Periodic turmoil in stock markets worldwide demonstrates the necessity for developing risk management tools that can be used to analyze the vast volume of information that is available. The DSS framework provides such tools that enable investors and portfolio managers to employ sophisticated techniques from the fields of statistical analysis, econometric analysis, and operations research to make and implement real-time portfolio management decisions.
Recent research in this field has been oriented towards combining the powerful analytical tools used in the DSS framework with the new modeling techniques provided by soft computing technology (neural networks, expert systems, fuzzy sets, etc.) to address the uncertainty, vagueness, and fuzziness that is often encountered in the financial and business environment.
SEE ALSO: Competitive Intelligence ; Computer Networks ; Computer-Aided Design and Manufacturing ; Management Information Systems ; Strategic Planning Tools
Constantin Zopounidis and
Michael Doumpos
Revised by Laurie Hillstrom
FURTHER READING:
Elton, E.J., and M.J. Gruber. Modern Portfolio Theory and Investment Analysis. 5th ed. New York: John Wiley and Sons, 1995.
Markowitz, H. Portfolio Selection: Efficient Diversification of Investments. New York: John Wiley and Sons, 1959.
Phillips-Wren, Gloria E., et al., "A Multiple-Criteria Framework for Evaluation of Decision Support Systems." Omega. August 2004.
Turban, Efraim, et al. Decision Support Systems and Intelligent Systems. 7th ed. Englewood Cliffs, NJ: Prentice Hall, 2004.
Zopounidis, C., M. Godefroid, and C. Hurson. "Designing a Multicriteria DSS for Portfolio Selection and Management." In Advances in Stochastic Modelling and Data Analysis. edited by J. Janssen, C.H. Skiadas and C. Zopounidis. Dordrecht, Netherlands: Kluwer Academic Publishers, 1995, 261–292.
Comment about this article, ask questions, or add new information about this topic: