ZERO SUM GAME
A zero-sum game is a term used in connection with game theory and management games. Game theory is a mathematical theory that applies to certain situations in which there are conflicts of interest between two or more individuals or groups. Management games are training or educational activities utilizing game theory models consisting of work situations. A zero-sum game is one type of management game in which all the payoffs for all players total zero; what one player or group gains, the other loses.
To better understand the term zero-sum game, it is beneficial to analyze game theory, as well as management games. Game theory is a significant branch of operations research and is closely related to decision theory and operational gaming. It attempts to answer the question, In a situation of conflict, what choice should the player make?
Game theory deals with abstract models of conflict situations or games of strategy. A game occurs when an individual or teams of people are in competition either against one another or against situations, or both.
A game can be represented by the following model:
- there are n players ( n being a certain number), each of whom is required to make one choice from a specified set of possible choices;
- when every player has made a choice, the particular combination of choices they have made determines an outcome that, in some way, affects or interests all players;
- each player knows what outcome results from each possible combination of choices;
- each player has an order of preference for the possible outcomes (often each player assigns to each outcome a numerical value, called a payoff, which can be thought of as representing the number of points, or dollars, etc., that he gains or loses from the outcome);
- each player knows the preferences of the other players (she knows what their payoffs are) and all players are assumed to act so as to gain the most they can from the game; but
- each player makes his choice without knowing what choice the other players are making.
In the game, the competing players are identified as persons whether they are individuals, teams, or any other group representing a single set of interests. A play of a game is an exercise of the conflict model according to the rules; it consists of one or more moves by each player and may involve moves left to chance. The outcome of the game is represented by the payoff, a gain or loss of some utility to each of the players as a result of the positions reached at the end of the game. The solution of a game is comprised of the identification from among all the possible alternative courses of action, which ensures the player's expected payoff at a quantity called the value of the game.
In a business scenario, for example, the competition between two companies may be structured in game-theory terms. The persons are the companies, the play can be a determined period of time; and the rules are the discipline of the marketplace. Within the rules, management may make a variety of decisions upon which actions may be taken. These are known as the moves.
The firm's master plan is the strategy. In this example, the strategies of the companies would describe the companies' general decisions on such topics as advertising, mergers, and new product lines. The results of the interactions among the strategic choices made by the two firms are manifested by the payoff, which could be chosen to be annual gross sales, net profits, and so on. Only when a situation such as this is structured and quantified is it meaningful to address a solution and value for the game. The theory is used to calculate the optimum strategy that maximizes the winnings or minimizes the losses of one or more of the players.
Finite games, those in which each player has available a finite number of strategies, may be categorized according to the number of persons, relationships among payoffs, and whether cooperation among the players is allowed. The simplest form is the two-person zero-sum game, zero-sum denoting that the sum of the payoffs to the two players is zero.
A payoff matrix can be arranged to identify the payoffs for each player. The matrix is expressed in terms of the payoff to A, whereas B's payoffs are the negative of A's, thus satisfying the condition that their sum be zero. Positive entries indicate payments by B to A; negative ones, payments by A to B.
The solution can take two forms; the pure strategy case, in which a single strategy will be indicated as optimal; or a mixed strategy case, in which two or more strategies appear along with the relative frequencies with which they must be employed. An example of a two-person zero-sum game given by Derek French and Heather Saward, showing a pure strategy solution, is presented in Exhibit 1.
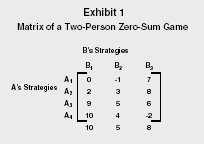
Matrix of a Two-Person Zero-Sum Game
A's problem is to choose one of his four strategies; while B's is to choose one of his three. For example, the choices of A2 and B2 result in the payment by B to A of three units, while A4 and B3 lead to the payment by A to B of two units. First, consider A's analysis of his problem: A1 is a weak strategy because it nets A less than does the equally available strategy A2, regardless of B's choice. In this example, A1 is dominated by A2, and hence A1 from further consideration. By choosing A4 in an effort to realize the payoff of ten units at A4 and B1 could result in the loss of two units if B selects B3; similar dilemmas exist for the other choices.
Suppose that A takes a conservative point of view and examines the least his choice could produce; a gain of two for A2, a gain of five for A3, and a loss of two for A4. Of these options, A3 and its consequence appear the best choice; the five-unit gain represents an assured security level to A since he cannot be driven below this point by any action taken by B. In essence, A has examined the minimum gain that each row strategy could produce and, striving to maximize his gain has selected the greatest of these.
This is referred to as A's maximum strategy (R3 in Exhibit 1). At this point, B analyzes the greatest loss he might sustain as a result of his strategy choice; ten units for B1, five units for B2, and eight units for B3. Of these choices, B2 causes the smallest loss on B and establishes his security level by guaranteeing that no action of A's can cause his loss to be above five.
Summarizing, B has identified the maximum loss that each column strategy could produce and, wanting to minimize his loss has selected the least of these; known as B's minimax strategy. The most important feature of this result is the independently arrived-at agreement on the part of the players as to their security levels. This example also possesses a saddle-point, an element that is concurrently the greatest of the row minima and the least of the column maxima. The significance lies in the fact that if either player deviates from this choice; it will result in either decreased gain or increased loss.
The solution is that A always employs A3, B always employs B2, and the value of the game is five. This, of course, is not a fair game since A always wins five units at each play. It can be made fair, however, by requiring A to pay five units to B each time to induce B to play, or by reducing each element of the game matrix by five.
In recent years there has been opportunity to watch game strategies being used on the reality television shows that place teams, and eventually individuals, against each other. While ultimately a zero-sum game (in the end, one person wins everything), successful participants employed various strategies to cooperate with and exploit each other, all in an effort to win.
Although the most notorious use of game theory was utilized by the armed services in the Vietnam War for strategic purposes, the theory is noted today for its potential contribution to industrial affairs. Game theory is used to analyze economic policies and international agreements (e.g., whether economic sanctions act as practical incentives or build additional resentment). It is applied in management games, in which managers are grouped into teams representing a manager or the management of one of several competing organizations. The manager must take a sequence of decisions relating to a simulation of a real-life management problem, and is then presented with the results of each decision after it is made.
In the game, the result of an individual decision is the response, or the next move, of the other competitors. The games are used for several training purposes. They provide experience and they bring rapid feedback on the results of a decision. They also can show cause-and-effect relationships that may be blurred during longer time periods in real-life situations. The end result is to attain more personal involvement, greater attention, and greater retention of new concepts and ideas that have been acquired.
SEE ALSO: Decision Making
Kevin Nelson
Revised by Wendy H. Mason
FURTHER READING:
Finch, Frank, ed. The Facts on File Encyclopedia of Management Techniques. New York, NY: Facts on File, 1985.
French, Derek, and Heather Saward. Dictionary of Management. Aldershot, Hants, England: Gower, 1983.
"Game Theory." Asia Africa Intelligence Wire, 29 August 2004.
McMillan, John. Games, Strategies and Managers. New York, NY: Oxford University Press, 1996.
Poundstone, William. Prisoners' Dilemma. New York, NY: Anchor Books, Doubleday, 1993.
Comment about this article, ask questions, or add new information about this topic: