STATISTICS

Statistics is a field of knowledge that enables an investigator to derive and evaluate conclusions about a population from sample data. In other words, statistics allow us to make generalizations about a large group based on what we find in a smaller group.
The field of statistics deals with gathering, selecting, and classifying data; interpreting and analyzing data; and deriving and evaluating the validity and reliability of conclusions based on data.
Strictly speaking, the term "parameter" describes a certain aspect of a population, while a "statistic" describes a certain aspect of a sample (a representative part of the population). In common usage, most people use the word "statistic" to refer to research figures and calculations, either from information based on a sample or an entire population.
Statistics means different things to different people. To a baseball fan, statistics are information about a pitcher's earned run average or a batter's slugging percentage or home run count. To a plant manager at a distribution company, statistics are daily reports on inventory levels, absenteeism, labor efficiency, and production. To a medical researcher investigating the effects of a new drug, statistics are evidence of the success of research efforts. And to a college student, statistics are the grades made on all the exams and quizzes in a course during the semester. Today, statistics and statistical analysis are used in practically every profession, and for managers in particular, statistics have become a most valuable tool.
A set of data is a population if decisions and conclusions based on these data can be made with absolute certainty. If population data is available, the risk of arriving at incorrect decisions is completely eliminated.
But a sample is only part of the whole population. For example, statistics from the U.S. Department of Commerce suggest that as of April 2005, 10.1 percent of rental homes and apartments were vacant. However, the data used to calculate this vacancy rate was not derived from all owners of rental property, but rather only a segment ("sample" in statistical terms) of the total group (or "population") of rental property owners. A population statistic is thus a set of measured or described observations made on each elementary unit. A sample statistic, in contrast, is a measure based on a representative group taken from a population.
QUANTITATIVE AND QUALITATIVE
STATISTICS
Measurable observations are called quantitative observations. Examples of measurable observations include the annual salary drawn by a BlueCross/BlueShield underwriter or the age of a graduate student in an MBA program. Both are measurable and are therefore quantitative observations.
Observations that cannot be measured are termed qualitative. Qualitative observations can only be described. Anthropologists, for instance, often use qualitative statistics to describe how one culture varies from another. Marketing researchers have increasingly used qualitative statistical techniques to describe phenomena that are not easily measured, but can instead be described and classified into meaningful categories. Here, the distinction between a population of variates (a set of measured observations) and a population of attributes (a set of described observations) is important.
Values assumed by quantitative observations are called variates. These quantitative observations are further classified as either discrete or continuous. A discrete quantitative observation can assume only a limited number of values on a measuring scale. For example, the number of graduate students in an MBA investment class is considered discrete.
Some quantitative observations, on the other hand, can assume an infinite number of values on a measuring scale. These quantitative measures are termed continuous. How consumers feel about a particular brand is a continuous quantitative measure; the exact increments in feelings are not directly assignable to a given number. Consumers may feel more or less strongly about the taste of a hamburger, but it would be difficult to say that one consumer likes a certain hamburger twice as much as another consumer.
DESCRIPTIVE AND INFERENTIAL
STATISTICS
Managers can apply some statistical technique to virtually every branch of public and private enterprise. These techniques are commonly separated into two broad categories: descriptive statistics and inferential statistics. Descriptive statistics are typically simple summary figures calculated from a set of observations. Suppose a professor computes an average grade for one accounting class. If the professor uses the statistic simply to describe the performance of that class, the result is a descriptive statistic of overall performance.
Inferential statistics are used to apply conclusions about one set of observations to reach a broader conclusion or an inference about something that has not been directly observed. In this case, a professor might use the average grade from a series of previous accounting classes to estimate, or infer, the average grade for future accounting classes. Any conclusion made about future accounting classes is based solely on the inferential statistics derived from previous accounting classes.
FREQUENCY DISTRIBUTION
Data is a collection of any number of related observations. A collection of data is called a data set. Statistical data may consist of a very large number of observations. The larger the number of observations, the greater the need to present the data in a summarized form that may omit some details, but reveals the general nature of a mass of data.
Frequency distribution allows for the compression of data into a table. The table organizes the data into classes or groups of values describing characteristics of the data. For example, students' grade distribution is one characteristic of a graduate class.
A frequency distribution shows the number of observations from the data set that fall into each category describing this characteristic. The relevant categories are defined by the user based on what he or she is trying to accomplish; in the case of grades, the categories might be each letter grade (A, B, C, etc.), pass/fail/incomplete, or grade percentage ranges. If you can determine the frequency with which values occur in each category, you can construct a frequency distribution. A relative frequency distribution presents frequencies in terms of fractions or percentages. The sum of all relative frequency distributions equals 1.00 or 100 percent.
Table 1 illustrates both a frequency distribution and a relative frequency distribution. The frequency distribution gives a break down of the number of
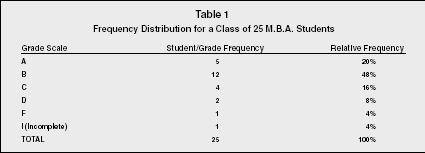
Frequency Distribution for a Class of 25 M.B.A. Students
| Grade Scale | Student/Grade Frequency | Relative Frequency |
| A | 5 | 20% |
| B | 12 | 48% |
| C | 4 | 16% |
| D | 2 | 8% |
| F | 1 | 4% |
| I (Incomplete) | 1 | 4% |
| TOTAL | 25 | 100% |
students in each grade category ranging from A to F, including "I" for incomplete. The relative frequency distribution takes that number and turns it into a percentage of the whole number.
The chart shows us that five out of twenty-five students, or 25 percent, received an A in the class. It is basically two different ways of analyzing the same data. This is an example of one of the advantages of statistics. The same data can be analyzed several different ways.
PARAMETERS
Decisions and conclusions can often be made with absolute certainty if a single value that describes a certain aspect of a population is determined. As noted earlier, a parameter describes an entire population, whereas a statistic describes only a sample. The following are a few of the most common types of parameter measurements used.
AGGREGATE PARAMETER.
An aggregate parameter can be computed only for a population of variates. The aggregate is the sum of the values of all the variates in the population. Industry-wide sales is an example of an aggregate parameter.
PROPORTION.
A proportion refers to a fraction of the population that possesses a certain property. The proportion is the parameter used most often in describing a population of attributes, for example, the percentage of employees over age fifty.
ARITHMETIC MEAN.
The arithmetic mean is simply the average. It is obtained by dividing the sum of all variates in the population by the total number of variates. The arithmetic mean is used more often than the median and mode to describe the average variate in the population. It best describes the values such as the average grade of a graduate student, the average yards gained per carry by a running back, and the average calories burned during a cardiovascular workout. It also has an interesting property: the sum of the deviations of the individual variates from their arithmetic mean is always is equal to zero.
MEDIAN.
The median is another way of determining the "average" variate in the population. It is especially useful when the population has a particularly skewed frequency distribution; in these cases the arithmetic mean can be misleading.
To compute the median for a population of variates, the variates must be arranged first in an increasing or decreasing order. The median is the middle variate if the number of the variates is odd. For example, if you have the distribution 1, 3, 4, 8, and 9, then the median is 4 (while the mean would be 5). If the number of variates is even, the median is the arithmetic mean of the two middle variates. In some cases (under a normal distribution) the mean and median are equal or nearly equal. However, in a skewed distribution where a few large values fall into the high end or the low end of the scale, the median describes the typical or average variate more accurately than the arithmetic mean does.
Consider a population of four people who have annual incomes of $2,000, $2,500, $3,500, and $300,000—an extremely skewed distribution. If we looked only at the arithmetic mean ($77,000), we would conclude that it is a fairly wealthy population on average. By contrast, in observing the median income ($3,000) we would conclude that it is overall a quite poor population, and one with great income disparity. In this example the median provides a much more accurate view of what is "average" in this population because the single income of $300,000 does not accurately reflect the majority of the sample.
MODE.
The mode is the most frequently appearing variate or attribute in a population. For example, say a class of thirty students is surveyed about their ages. The resulting frequency distribution shows us that ten students are 18 years old, sixteen students are 19 years old, and four are 20 or older. The mode for this group would be the sixteen students who are 19 years old. In other words, the category with the most students is age 19.
MEASURE OF VARIATION
Another pair of parameters, the range and the standard deviation, measures the disparity among values of the various variates comprising the population. These parameters, called measures of variation, are designed to indicate the degree of uniformity among the variates.
The range is simply the difference between the highest and lowest variate. So, in a population with incomes ranging from $15,000 to $45,000, the range is $30,000 ($45,000 - $15,000 = $30,000).
The standard deviation is an important measure of variation because it lends itself to further statistical analysis and treatment. It measures the average amount by which variates are spread around the mean. The standard deviation is a versatile tool based on yet another calculation called the variance. The variance for a population reflects how far data points are from the mean, but the variance itself is typically used to calculate other statistics rather than for direct interpretation, such as the standard deviation, which is more useful in making sense of the data.
The standard deviation is a simple but powerful adaptation of the variance. It is found simply by taking the square root of the variance. The resulting figure can be used for a variety of analyses. For example, under a normal distribution, a distance of two standard deviations from the mean encompasses approximately 95 percent of the population, and three standard deviations cover 99.7 percent.
Thus, assuming a normal distribution, if a factory produces bolts with a mean length of 7 centimeters (2.8 inches) and the standard deviation is determined to be 0.5 centimeters (0.2 inches), we would know that 95 percent of the bolts fall between 6 centimeters (2.4 inches) and 8 centimeters (3.1 inches) long, and that 99.7 percent of the bolts are between 5.5 centimeters (2.2 inches) and 8.5 centimeters (3.3 inches). This information could be compared to the product specification tolerances to determine what proportion of the output meets quality control standards.
PROBABILITY
Modern statistics may be regarded as an application of the theory of probability. A set is a collection of well-defined objects called elements of the set. The set may contain a limited or infinite number of elements. The set that consists of all elements in a population is referred to as the universal set.
Statistical experiments are those that contain two significant characteristics. One is that each experiment has several possible outcomes that can be specified in advance. The second is that we are uncertain about the outcome of each experiment. Examples of statistical experiments include rolling a die and tossing a coin. The set that consists of all possible outcomes of an experiment is called a sample space, and each element of the sample space is called a sample point.
Each sample point or outcome of an experiment is assigned a weight that measures the likelihood of its occurrence. This weight is called the probability of the sample point.
Probability is the chance that something will happen. In assigning weights or probabilities to the various sample points, two rules generally apply. The first is that probability assigned to any sample point ranges from 0 to 1. Assigning a probability of 0 means that something can never happen; a probability of 1 indicates that something will always happen. The second rule is that the sum of probabilities assigned to all sample points in the sample space must be equal to 1 (e.g., in a coin flip, the probabilities are .5 for heads and .5 for tails).
In probability theory, an event is one or more of the possible outcomes of doing something. If we toss a coin several times, each toss is an event. The activity that produces such as event is referred to in probability theory as an experiment. Events are said to be mutually exclusive if one, and only one, can take place at a time. When a list of the possible events that can result from an experiment includes every possible outcome; the list is said to be collectively exhaustive. The coin toss experiment is a good example of collective exhaustion. The end result is either a head or a tail.
There are a few theoretical approaches to probability. Two common ones are the classical approach and the relative frequency approach. Classical probability defines the probability that an event will occur as the number of outcomes favorable to the occurrence of the event divided by the total number of possible outcomes. This approach is not practical to apply in managerial situations because it makes assumptions that are unrealistic for many real-life applications. It assumes away situations that are very unlikely, but that could conceivably happen. It is like saying that when a coin is flipped ten times, there will always be exactly five heads and five tails. But how many times do you think that actually happens? Classical probability concludes that it happens every time.
The relative frequency approach is used in the insurance industry. The approach, often called the relative frequency of occurrence, defines probability as the observed relative frequency of an event in a very large number of trials, or the proportion of times that an event occurs in the long run when conditions are stable. It uses past occurrences to help predict future probabilities that the occurrences will happen again.
Actuaries use high-level mathematical and statistical calculations in order to help determine the risk that some people and some groups might pose to the insurance carrier. They perform these operations in order to get a better idea of how and when situations that would cause customers to file claims and cost the company money might occur. The value of this is that it gives the insurance company an estimate of how much to charge for insurance premiums. For example, customers who smoke cigarettes are in higher risk group than those who do not smoke. The insurance company charges higher premiums to smokers to make up for the added risk.
SAMPLING
The objective of sampling is to select that part which is representative of the entire population. Sample designs are classified into probability samples and nonprobability samples. A sample is a probability sample if each unit in the population is given some chance of being selected. The probability of selecting each unit must be known. With a probability sample, the risk of incorrect decisions and conclusions can be measured using the theory of probability.
A sample is a non-probability sample when some units in the population are not given any chance of being selected, and when the probability of selecting any unit into the sample cannot be determined or is not known. For this reason, there is no means of measuring the risk of making erroneous conclusions derived from non-probability samples. Since the reliability of the results of non-probability samples cannot be measured, such samples do not lend themselves to statistical treatment and analysis. Convenience and judgment samples are the most common types of non-probability samples.
Among its many other applications, sampling is used in some manufacturing and distributing settings as a means of quality control. For example, a sample of 5 percent may be inspected for quality from a predetermined number of units of a product. That sample, if drawn properly, should indicate the total percentage of quality problems for the entire population, within a known margin of error (e.g., an inspector may be able to say with 95 percent certainty that the product defect rate is 4 percent, plus or minus 1 percent).
In many companies, if the defect rate is too high, then the processes and machinery are checked for errors. When the errors are found to be human errors, then a statistical standard is usually set for the acceptable error percentage for laborers.
In sum, samples provide estimates of what we would discover if we knew everything about an entire population. By taking only a representative sample of the population and using appropriate statistical techniques, we can infer certain things, not with absolute precision, but certainly within specified levels of precision.
SEE ALSO: Data Processing and Data Management ; Forecasting ; Models and Modeling ; Planning
James C. Koch
Revised by Scott Droege
FURTHER READING:
Anderson, David, Dennis Sweeney, and Thomas Williams. Essentials of Statistics for Business and Economics. Thomson South-Western, 2006.
Hogg, Robert, and Elliot Tanas. Probability and Statistical Inference. 7th ed. Upper Saddle River, NJ: Prentice Hall, 2005.
(2)The household in Lilongwe are to be sampled in order to estimate the average amount of assets per household that are readily convertible into cash. The households are stratified into a high-rent and low-rent stratum. A house in a high-rent stratum is thought to have about nine times as much assets as one in a low-rent stratum. And a stratum size is expected to be proportional to the square root of the stratum mean. There are 4,000 households in the high-rent stratum and 20,000 in the low-rent stratum.
(a) How would you distribute a sample of 1,000 households between the two strata?
(b) If the objective is to estimate the difference between assets per household in the strata, how should the sample be distributed?
the average, amount of assets per household that are readily
convertible into cash. The households are stratified into a high-rent
and a low-rent stratum. A house in the high-rent stratum is
thought to have about nine times as much assets as one in the
low-rent stratum, and Sit is expected to be proportional to the
square root of the stratum mean.
There are 4000 households in the high-rent stratum and 20,000 in
the low-rent stratum.
a. How would you distribute a sample of 1000 households
between the two strata?
b. If the object is to estimate the difference between assets per
household in the two strata, how should the sample be
distributed?